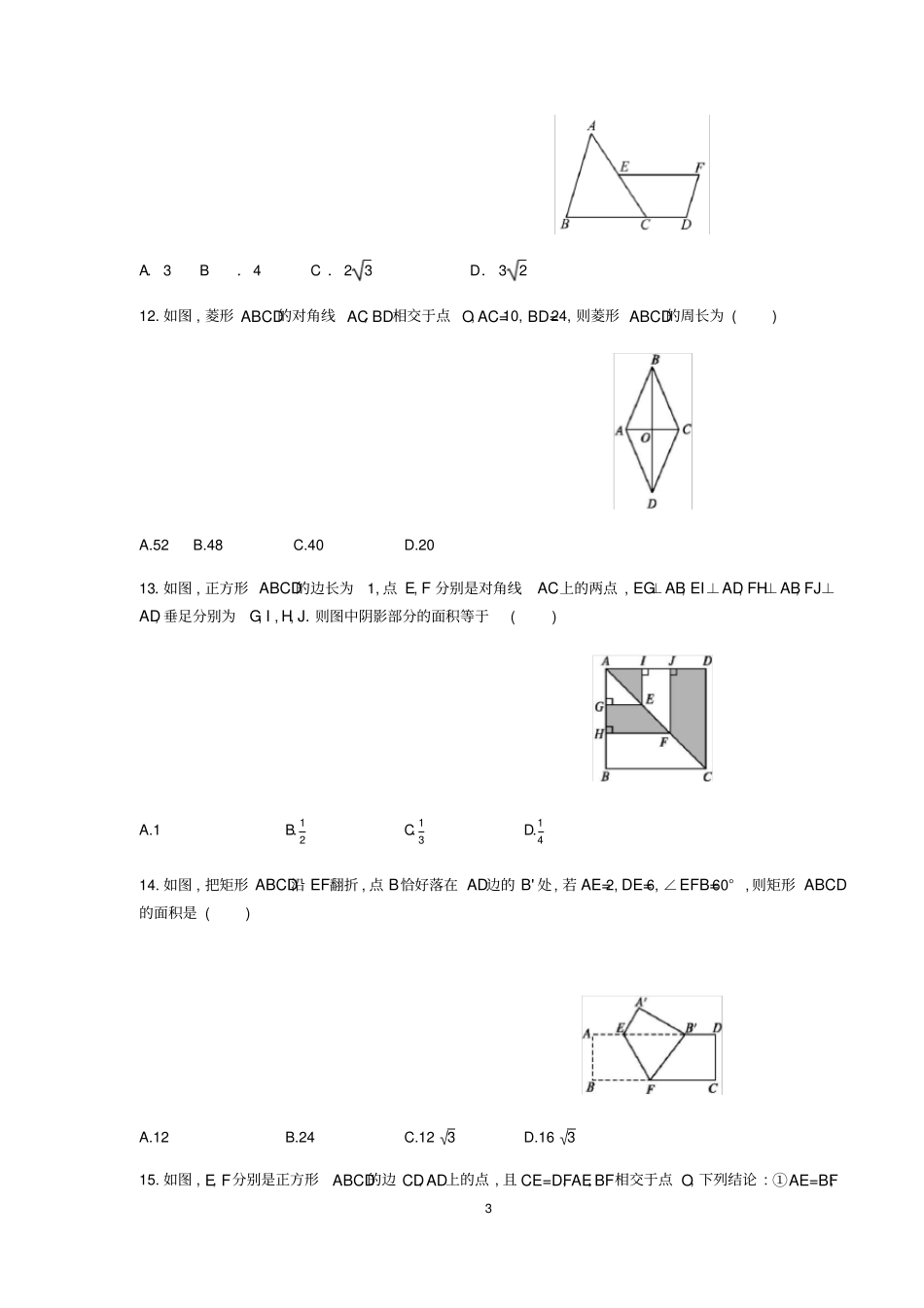
1第十八章平行四边形专题突破一、选择题(共23题)。1.在?ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是()A.BE=DFB.AE=CFC.AF∥CED.∠BAE=∠DCF2.在?ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定3.如图,?ABCD的对角线AC,BD相交于点O,E是AB的中点,且AE+EO=4,则?ABCD的周长为()A.20B.16C.12D.84.如图,在?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为()A.3B.6C.12D.245.如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为()A.50°B.40°C.30°D.20°6.若平行四边形的两条对角线长为6cm和16cm,则下列长度的线段可作为平行四边形边长的是()2A.5cmB.8cmC.12cmD.16cm7.顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD;②BC=AD;③∠A=∠C;④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有()A.5种B.4种C.3种D.1种8.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是()A.22B.20C.22或20D.189.如图,在?ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF,BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有()A.1个B.2个C.3个D.4个10.如图,矩形ABCD中,AB=3,BC=4,BE∥DF且BE与DF之间的距离为3,则AE的长度是()A.7B.38C.78D.5811.如图,在△ABC中,延长BC至D,使得CD=12BC.过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD.连结DF,若AB=8,则DF的长为()3A.3B.4C.23D.3212.如图,菱形ABCD的对角线AC,BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为()A.52B.48C.40D.2013.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于()A.1B.12C.13D.1414.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B'处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B.24C.12√3D.16√315.如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;4②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确的有()A.4个B.3个C.2个D.1个16.如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=12cm,EF=16cm,则边AD的长是()A.12cmB.16cmC.20cmD.28cm17.如图,点E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.418.如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为()5A.31°B.28°C.62°D.56°19.如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF,CF,CF与AB交于G.有以下结论:①AE=BC;②AF=CF;③BF2=FG·FC;④EG·AE=BG·AB.其中正确的个数是()A.1B.2C.3D.420.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()A.34B.716C.2-12D.2-121.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为()6A.60°B.67.5°C.75°D.54°22.下列说法,正确的有()①四边相等的四边形一定是菱形②顺次连结矩形各边中点形成的四边形一定是正方形③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分A.4个B.3个C.2个D.1个23..我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该...