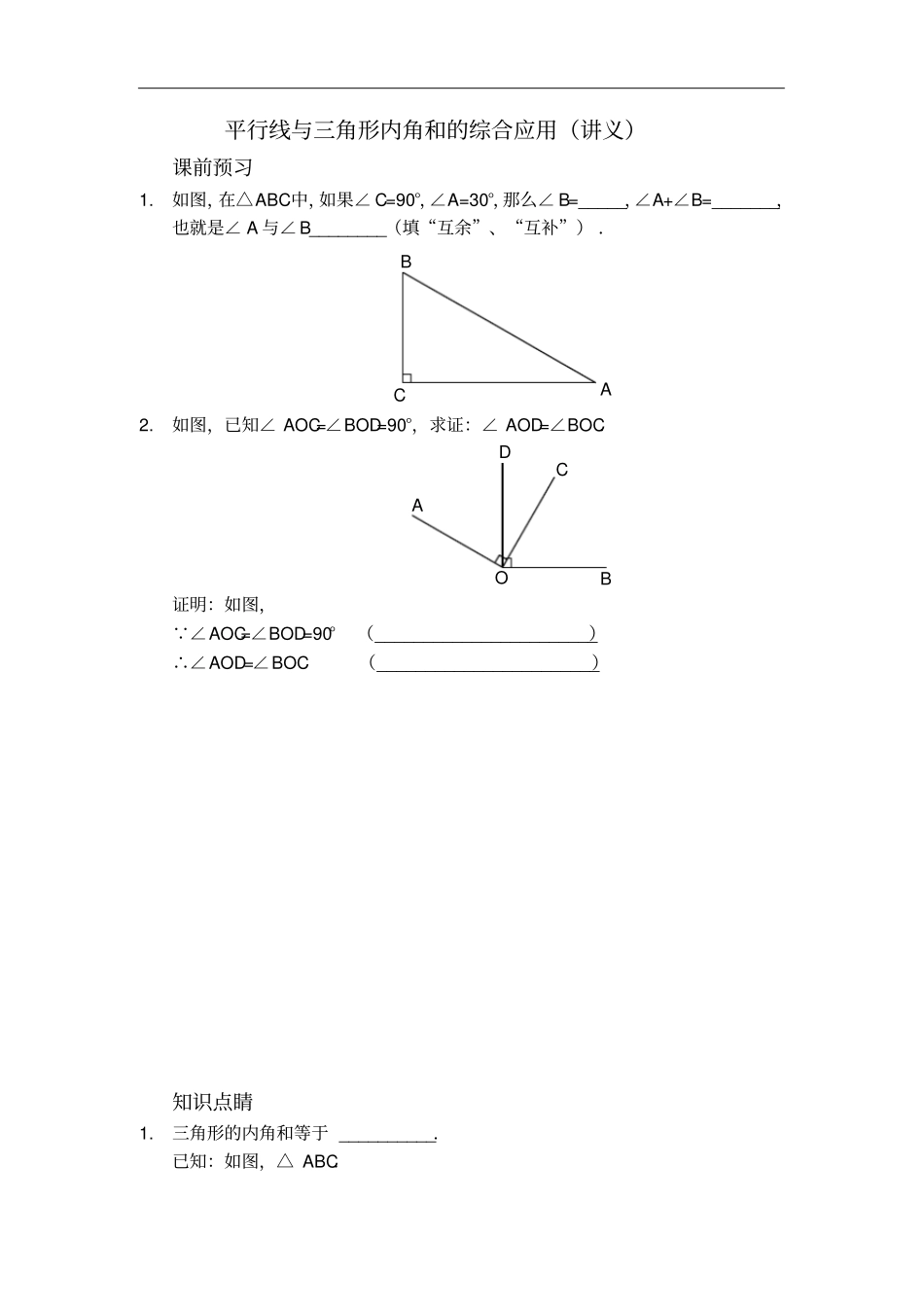
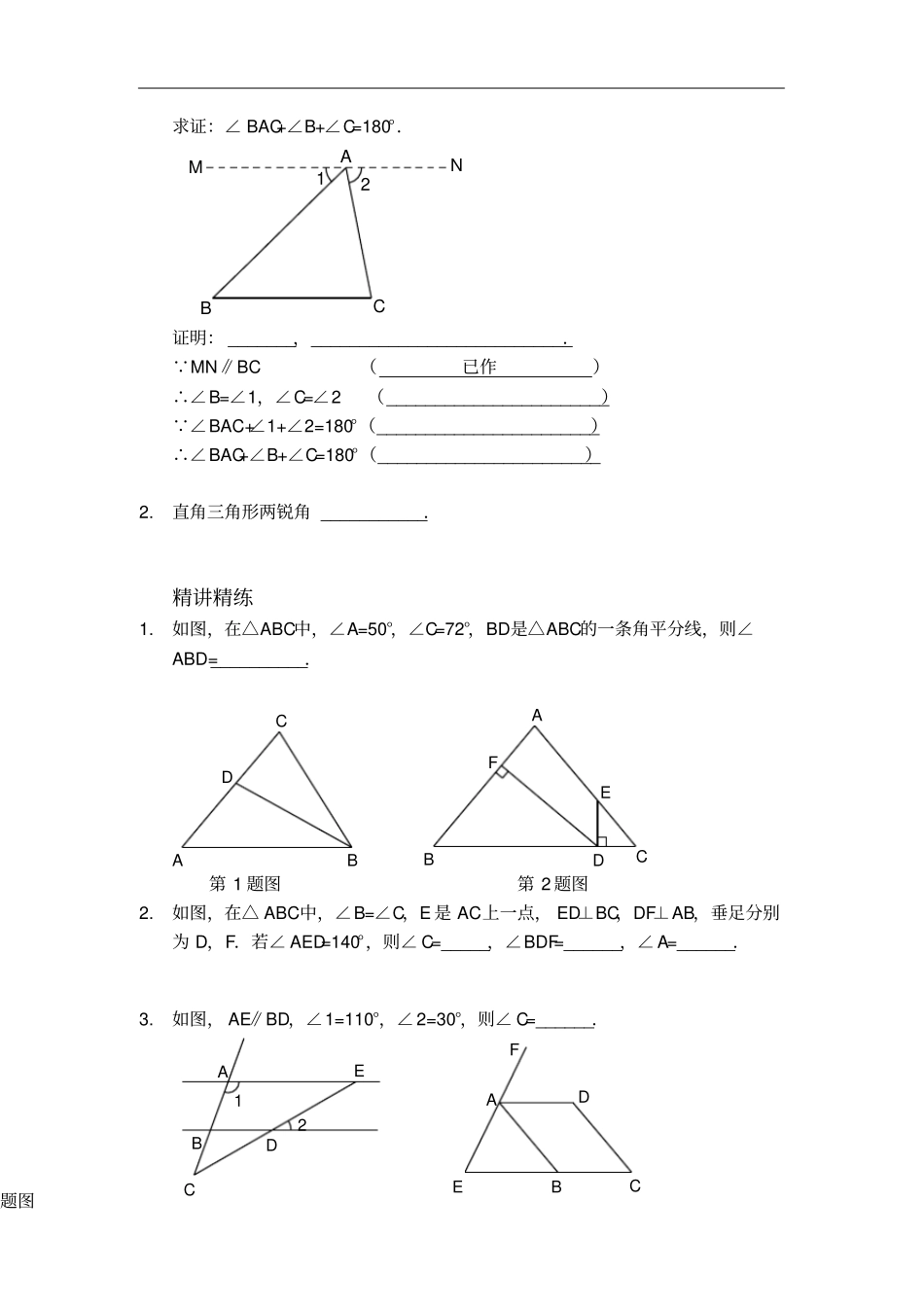
平行线与三角形内角和的综合应用(讲义)课前预习1.如图,在△ABC中,如果∠C=90°,∠A=30°,那么∠B=_____,∠A+∠B=_______,也就是∠A与∠B________(填“互余”、“互补”).ABC2.如图,已知∠AOC=∠BOD=90°,求证:∠AOD=∠BOC.DCBOA证明:如图,∵∠AOC=∠BOD=90°(_______________________)∴∠AOD=∠BOC(_______________________)知识点睛1.三角形的内角和等于__________.已知:如图,△ABC.求证:∠BAC+∠B+∠C=180°.AMBC12N证明:_______,___________________________.∵MN∥BC(已作)∴∠B=∠1,∠C=∠2(_______________________)∵∠BAC+∠1+∠2=180°(_______________________)∴∠BAC+∠B+∠C=180°(_______________________)2.直角三角形两锐角___________.精讲精练1.如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的一条角平分线,则∠ABD=__________.BDACFEDCBA第1题图第2题图2.如图,在△ABC中,∠B=∠C,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别为D,F.若∠AED=140°,则∠C=_____,∠BDF=______,∠A=______.3.如图,AE∥BD,∠1=110°,∠2=30°,则∠C=______.21EDCBAFDAEBC题图第3题图第4题图4.如图,AD∥BC,AB∥CD,E在CB的延长线上,EF经过点A,∠C=50°,∠FAD=60°,则∠EAB=_______.5.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=75°,∠ADE=35°,则∠EDC=_________.6.如图,在△ABC中,∠B=40°,∠BAC=68°,AD⊥BC于点D,求∠DAC的度数.解:如图,在△ABC中,∠B=40°,∠BAC=68°(已知)∴∠C=180°-______-______=180°-_____-_____=______(_______________________)∵AD⊥BC(已知)∴∠ADC=90°(垂直的定义)∴∠C+_____=90°(直角三角形两锐角互余)∴∠DAC=90°-______=90°-______=______(_______________________)7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.求证:∠A=∠BCD.证明:如图,∵∠ACB=90°(已知)∴∠A+_____=90°(直角三角形两锐角互余)∵CD⊥AB(已知)ABDCABCDEDCBA∴∠CDB=90°(垂直的定义)∴_____+∠B=90°(______________________)∴∠A=∠BCD(______________________)8.如图,在△ABC中,∠C=90°,点D是边AC上一点,DE∥BC,∠1=60°,求∠A的度数.ADE1BC9.如图,BD∥AE交△ABC的边AC于点F,∠CAE=95°,∠CBD=30°,求∠C的度数.ABCDEF10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB交CD于点E,交BC于点F.求证:∠1=∠2.【参考答案】课前预习1.60°,90°,互余2.已知,同角的余角相等知识点睛1.180°如图,过点A作MN∥BC两直线平行,内错角相等平角的定义等量代换2.互余精讲精练1.29°21FEDCBA2.50°,40°,80°3.40°4.70°5.35°6.解:如图,在△ABC中,∠B=40°,∠BAC=68°(已知)∴∠C=180°-∠B-∠BAC=180°-40°-68°=72°(三角形的内角和等于180°)∵AD⊥BC(已知)∴∠ADC=90°(垂直的定义)∴∠C+∠DAC=90°(直角三角形两锐角互余)∴∠DAC=90°-∠C=90°-72°=18°(等式的性质)7.证明:如图,∵∠ACB=90°(已知)∴∠A+∠B=90°(直角三角形两锐角互余)∵CD⊥AB(已知)∴∠CDB=90°(垂直的定义)∴∠BCD+∠B=90°(直角三角形两锐角互余)∴∠A=∠BCD(同角的余角相等)8.解:如图,∵DE∥BC(已知)∴∠1=∠B(两直线平行,同位角相等)∵∠1=60°(已知)∴∠B=60°(等量代换)∵∠C=90°(已知)∴∠A+∠B=90°(直角三角形两锐角互余)∴∠A=90°-∠B=90°-60°=30°(等式的性质)9.解:如图,∵BD∥AE(已知)∴∠CFD=∠CAE(两直线平行,同位角相等)∵∠CAE=95°(已知)∴∠CFD=95°(等量代换)∴∠CFB=180°-∠CFD=180°-95°=85°(平角的定义)在△CBF中,∠CBD=30°,∠CFB=85°(已知)∴∠C=180°-∠CBD-∠CFB=180°-30°-85°=65°(三角形的内角和等于180°)10.证明:如图,∵∠ACB=90°(已知)∴∠CAF+∠2=90°(直角三角形两锐角互余)∵CD⊥AB(已知)∴∠EDA=90°(垂直的定义)∴∠DAE+∠AED=90°(直角三角形两锐角互余)∵AF平分∠CAB(已知)∴∠CAF=∠DAE(角平分线的定义)∴∠2=∠AED(等角的余角相等)∵∠1=∠AED(对顶角相等)∴∠1=∠2(等量代换)