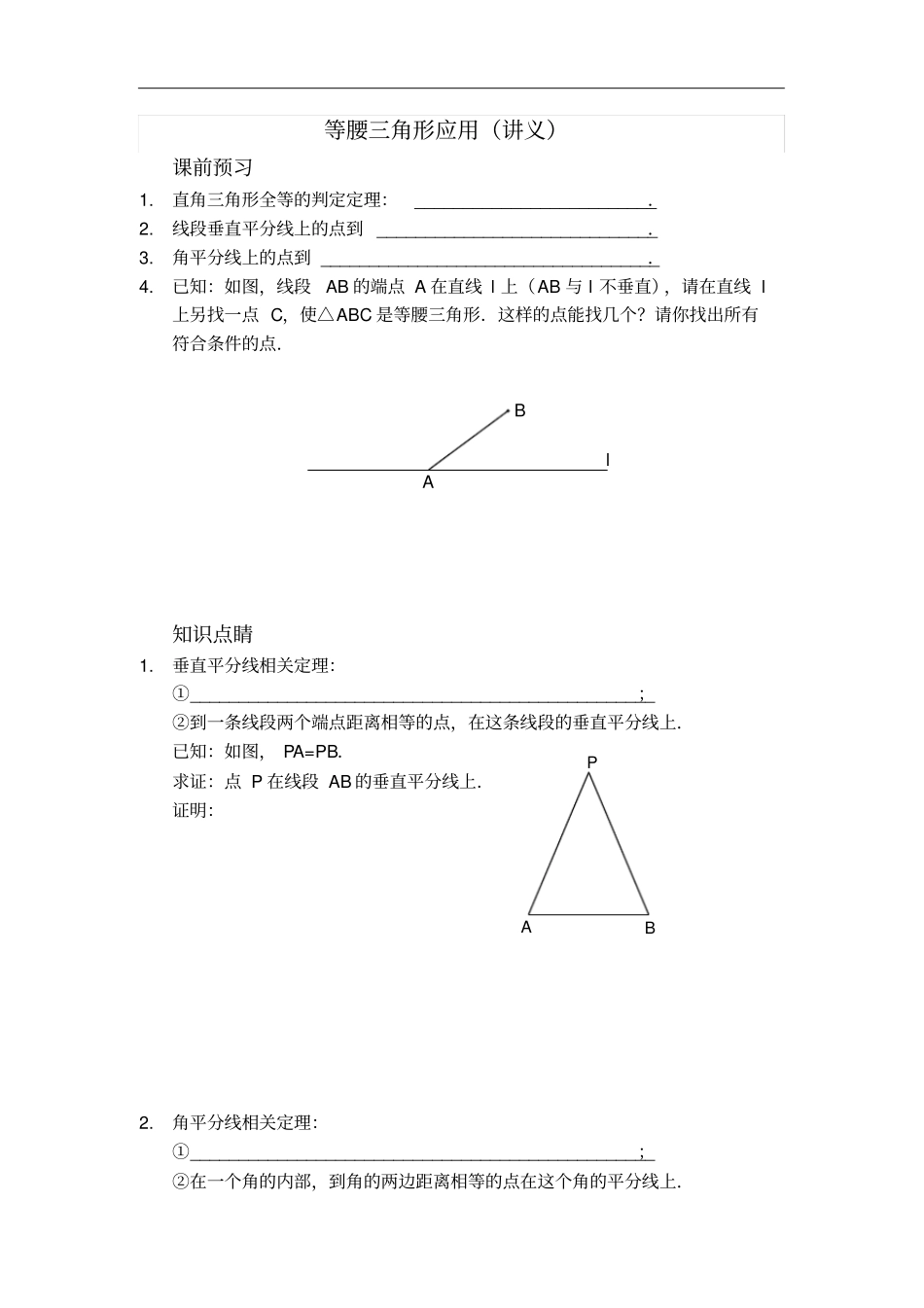
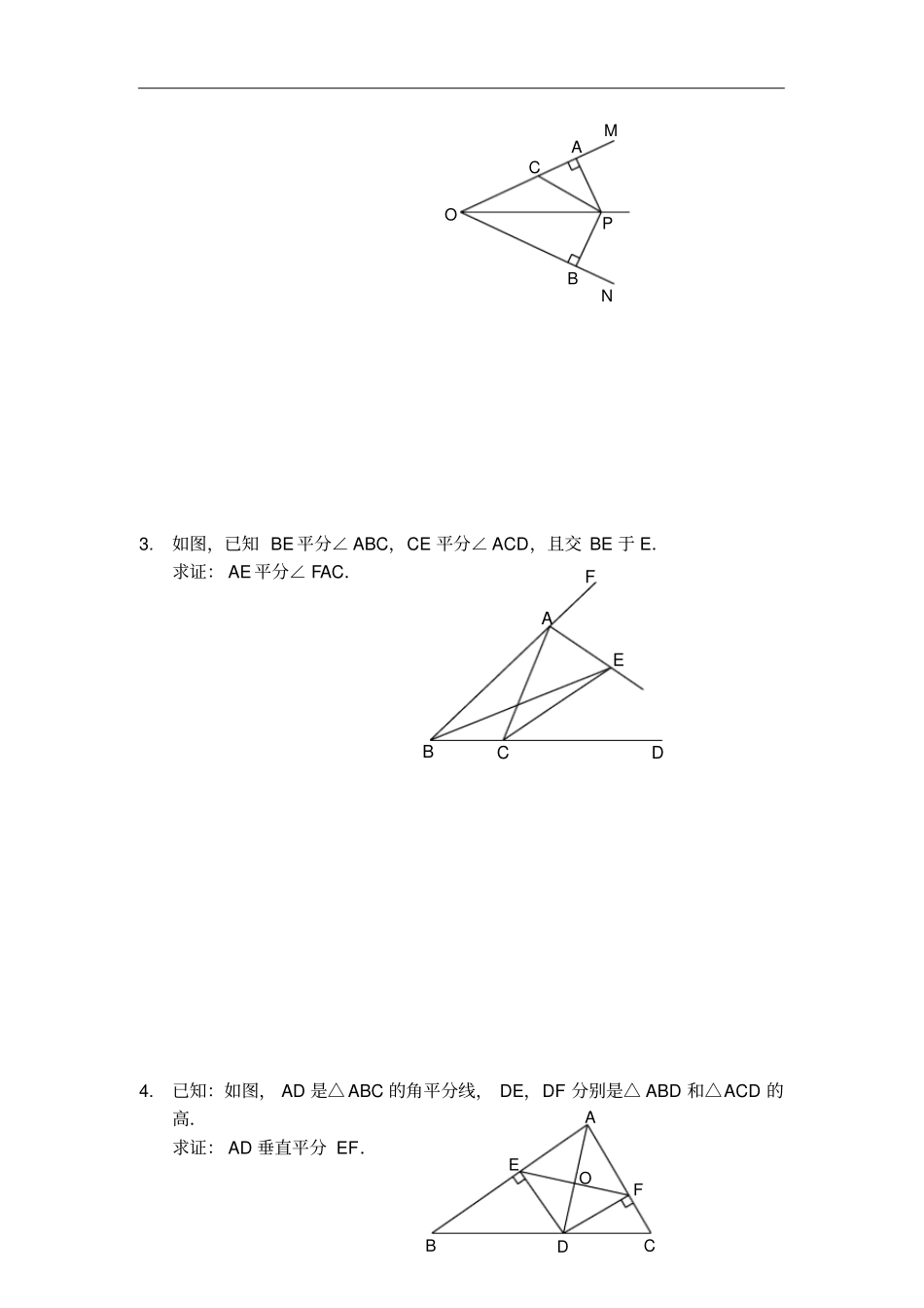
等腰三角形应用(讲义)课前预习1.直角三角形全等的判定定理:_________________________.2.线段垂直平分线上的点到_____________________________.3.角平分线上的点到___________________________________.4.已知:如图,线段AB的端点A在直线l上(AB与l不垂直),请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请你找出所有符合条件的点.lBA知识点睛1.垂直平分线相关定理:①________________________________________________;②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,PA=PB.求证:点P在线段AB的垂直平分线上.证明:2.角平分线相关定理:①________________________________________________;②在一个角的内部,到角的两边距离相等的点在这个角的平分线上.PBA已知:如图,点P在∠AOB内部,PC⊥OA于点C,PD⊥OB于点D,且PC=PD.求证:点P在∠AOB的平分线上.证明:3.在等腰三角形中,_________________,________________,______________重合(也称“__________”),这是等腰三角形的重要性质.若在一个三角形中,当中线,高线,角平分线“三线”中有“两线”重合时,则尝试构造___________.精讲精练1.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.求证:直线AO垂直平分线段BC.2.如图,已知PA⊥OM于A,PB⊥ON于B,且PA=PB.∠MON=50°,∠OPC=30°,求∠PCA的大小.PDCOBACBOAMNPCBOA3.如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.求证:AE平分∠FAC.4.已知:如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.求证:AD垂直平分EF.OFEDCBAFEDCBA5.如图,在△ABC中,点E在AB上,AE=AC,连接CE,点G为EC的中点,连接AG并延长交BC于D,连接ED,过点E作EF∥BC交AC于F.求证:EC平分∠DEF.6.已知:如图,D,E分别是AB,AC的中点,CD⊥AB于D,BE⊥AC于E,CD,BE交于点O.求证:AB=AC.GFEDCBAOEDCBA7.已知:如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于E,若CE=5cm,求BD的长.EDCBA8.如图,在△ABC中,延长BC到D,使CD=AC,连接AD,CE平分∠ACB,交AB于E,且AE=BE.求证:BC=CD.EDCBA9.在Rt△ABC中,∠C=90°,∠A=30°,若要在直线BC或AC上取一点P,使△ABP是等腰三角形,符合条件的点P有________个.CBA10.如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有________个.AB【参考答案】课前预习1.SAS,SSS,ASA,AAS,HL2.这条线段的两个端点的距离相等3.这个角的两边的距离相等4.这样的点有4个知识点睛1.线段垂直平分线上的点到这条线段的两个端点的距离相等2.角平分线上的点到这个角的两边距离相等3.顶角的平分线底边上的中线底边上的高三线合一等腰三角形精讲精练1.证明略(提示:利用等腰三角形“三线合一”)2.55°,证明略3.证明略(提示:过点E作EM⊥BF于M,EN⊥BD于N,EP⊥AC于P,证EP=EM)4.证明略(提示:利用等腰△DEF“三线合一”,证明AD垂直平分EF)5.证明略6.证明略(提示:连接BC,证△ABC是等边三角形)7.BD=10cm(提示:延长BA交CE的延长线于F,先证△BCF是等腰三角形,再证△ADB≌△AFC)8.证明略(提示:过点E作EF⊥AC于F,EG⊥BC于G,证明△ABC是等腰三角形)9.6个,作图略(两圆一线)10.8个,作图略(两圆一线)