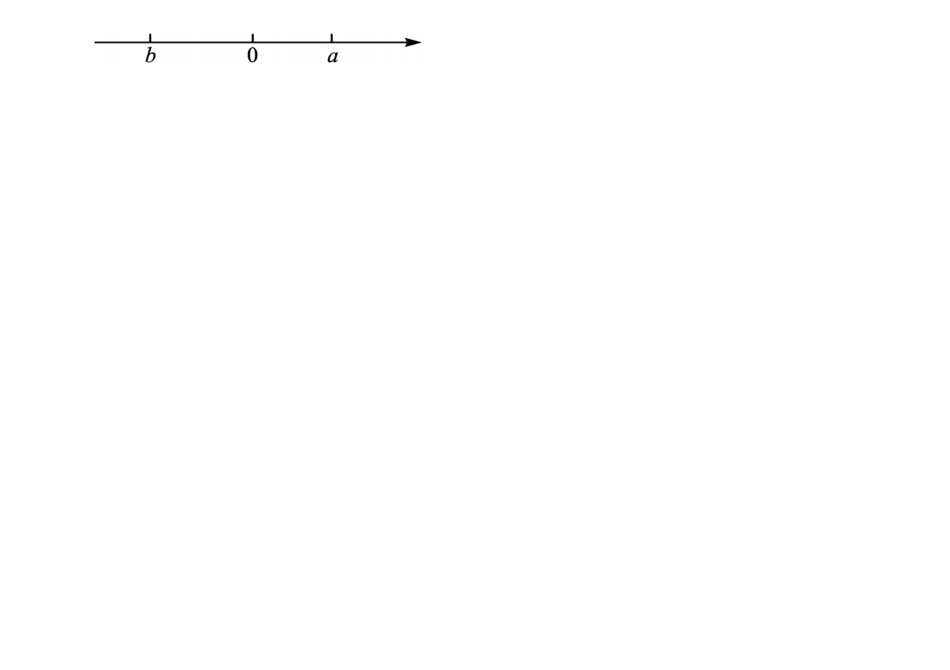
章末复习实数知识点1平方根、算术平方根、立方根的概念与性质1.(滨州中考)数5的算术平方根为()A.5B.25C.±25D.±52.下列说法中正确的是()A.-4没有立方根B.1的立方根是±1C.136的立方根是16D.-5的立方根是3-5.3.已知2a+1的算术平方根是0,b-a的算术平方根是12,求12ab的算术平方根.知识点2实数的分类与估算1.(烟台中考)下列实数中,有理数是()A.8B.34C.π2D.0.1010010012.下列语句中,正确的是()A.无理数都是无限小数B.无限小数都是无理数C.带根号的数都是无理数D.不带根号的数都是无理数3.估算17+4的值在()A.5和6之间B.6和7之间C.7和8之间D.8和9之间知识点3实数与数轴1.如图,下列各数中,数轴上点A表示的数可能是()A.4的算术平方根B.4的平方根C.8的算术平方根D.10的算术平方根2.如图,数轴上的两个点A,B所表示的数分别是a,b,在a+b,a-b,ab,|a|-|b|中,是正数的有1个.知识点4实数的性质及运算1.计算:3-22+23=.2.实数1-2的相反数是,绝对值是.3.求下列各式的值:(1)(5)2-22;(2)(-3)2+3-64;(3)121+7×2-17-31000.1.计算(-8)2的结果是()A.-8B.8C.16D.-162.下列各式正确的是()A.±31=±1B.4=±2C.(-6)2=-6D.3-27=33.下列说法中,正确的有()①只有正数才有平方根;②a一定有立方根;③-a没意义;④3-a=-3a;⑤只有正数才有立方根.A.1个B.2个C.3个D.4个4.(郾城区期中)如果一个实数的算术平方根等于它的立方根,那么满足条件的实数有()A.0个B.1个C.2个D.3个5.已知30.5≈0.7937,35≈1.7100,那么下列各式正确的是()A.3500≈17.100B.3500≈7.937C.3500≈171.00D.3500≈79.376.下列各组数中,互为倒数的一组是()A.5与-5B.2与12C.|-π|与(-π)2D.32与237.写出3-9到23之间的所有整数:.8.-27的立方根与81的平方根之和是.9.已知2a-1的平方根是±3,(-16)2的算术平方根是b,求a+b.10.已知a为250的整数部分,b-1是400的算术平方根,求a+b的值.综合题1.已知实数a,b在数轴上的位置如图所示,化简:|a-b|-a2+(-b)2+23b3.