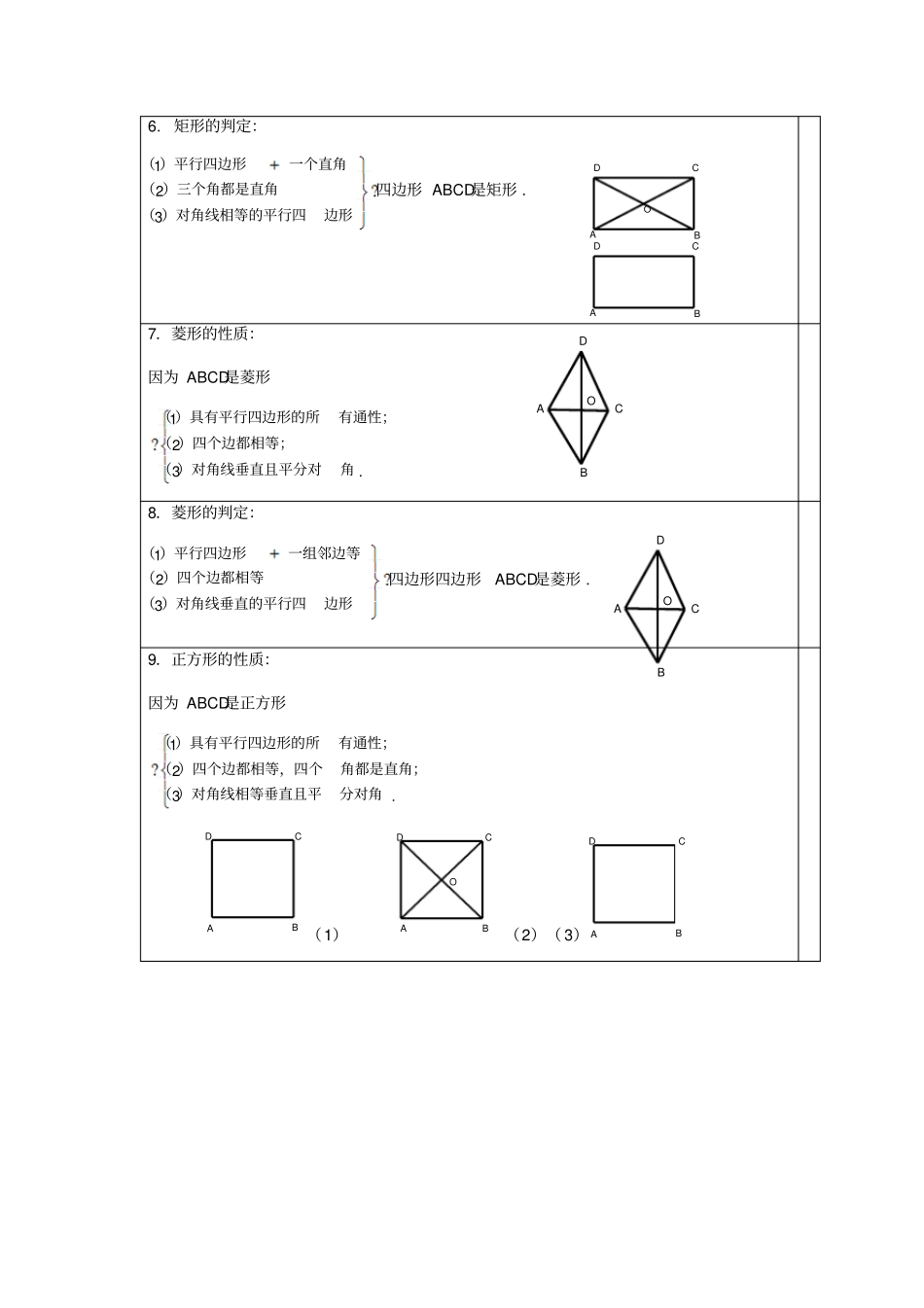
四边形1.四边形的内角和与外角和定理:(1)四边形的内角和等于360°;(2)四边形的外角和等于360°.2.多边形的内角和与外角和定理:(1)n边形的内角和等于(n-2)180°;(2)任意多边形的外角和等于360°.3.平行四边形的性质:因为ABCD是平行四边形.54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;(4.平行四边形的判定:是平行四边形)对角线互相平分()一组对边平行且相等()两组对角分别相等()两组对边分别相等()两组对边分别平行(ABCD54321.5.矩形的性质:因为ABCD是矩形.3;2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所(ABCD1234ABCDABDOCABDOCADBCADBCO6.矩形的判定:边形)对角线相等的平行四()三个角都是直角(一个直角)平行四边形(321四边形ABCD是矩形.7.菱形的性质:因为ABCD是菱形.321角)对角线垂直且平分对()四个边都相等;(有通性;)具有平行四边形的所(8.菱形的判定:边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321四边形四边形ABCD是菱形.9.正方形的性质:因为ABCD是正方形.321分对角)对角线相等垂直且平(角都是直角;)四个边都相等,四个(有通性;)具有平行四边形的所((1)(2)(3)CDABABCDOCDBAOCDBAOADBCADBCOCDAB10.正方形的判定:一组邻边等矩形)(一个直角)菱形(一个直角一组邻边等)平行四边形(321四边形ABCD是正方形.(3) ABCD是矩形又 AD=AB∴四边形ABCD是正方形14.三角形中位线定理:三角形的中位线平行第三边,并且等于它的一半.一基本概念:四边形,四边形的内角,四边形的外角,多边形,平行线间的距离,平行四边形,矩形,菱形,正方形,中心对称,中心对称图形,三角形中位线,梯形中位线.二定理:中心对称的有关定理※1.关于中心对称的两个图形是全等形.※2.关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分.※3.如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称.三公式:1.S菱形=21ab=ch.(a、b为菱形的对角线,c为菱形的边长,h为c边上的高)2.S平行四边形=ah.a为平行四边形的边,h为a上的高)四常识:※1.若n是多边形的边数,则对角线条数公式是:2)3n(n.2.规则图形折叠一般“出一对全等,一对相似”.3.如图:平行四边形、矩形、菱形、正方形的从属关系.4.常见图形中,仅是轴对称图形的有:角、等腰三角形、等边三角形、正奇边形、等腰梯形⋯⋯;仅是中心对称图形的有:平行四边形⋯⋯;是双对称图形的有:线段、矩形、菱形、正方形、正偶边形、圆⋯⋯.注意:线段有两条对称轴.平行四边形1(1)如图,□ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BC=6cm,则OE的长为※cm.(2)如图,□ABCD的对角线AC、BD相交于点O,点E是CD的中点,若AD=4cm,则OE的长为※cm.2如图,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,则图中全等三角形共有(※).(A)2对(B)3对(C)4对(D)5对4.(1)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能..判定这个四边形是平行四边形的是(※).(A)ABDCADBC∥,∥(B)ABDCADBC,(C)AOCOBODO,(D)ABDCADBC∥,(2)下列结论中,不正确的是(※).(A)对角线互相垂直的平行四边形是菱形;(B)对角线相等的平行四边形是矩形;FEDCAB(第8题)DECBA(第13题)ODCBA(第9题)DECBAO(第13题)(C)一组对边平行,一组对边相等的四边形是平行四边形;(D)对角线互相垂直的四边形面积等于对角线乘积的一半.(3).用两个全等的等边三角形,可以拼成下列哪种图形(※).(A)菱形(B)矩形(C)矩形和菱形(D)正方形5.(本小题满分6分)如图所示,把一幅直角三角板摆放在一起,30ACB,45BCD,90ABCBDC,量得20CDcm,试求BC、AC的长.6(1)如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并说明理由;(2)若AB=4,BC=6,求四边形OCED的周长和面积.(2)(本小题满分7分)(第18题)DBACDCBAOE(第21题)如图,在□ABCD中,对角线AC、BD相交于...