高二空间几何体练习题VIP免费

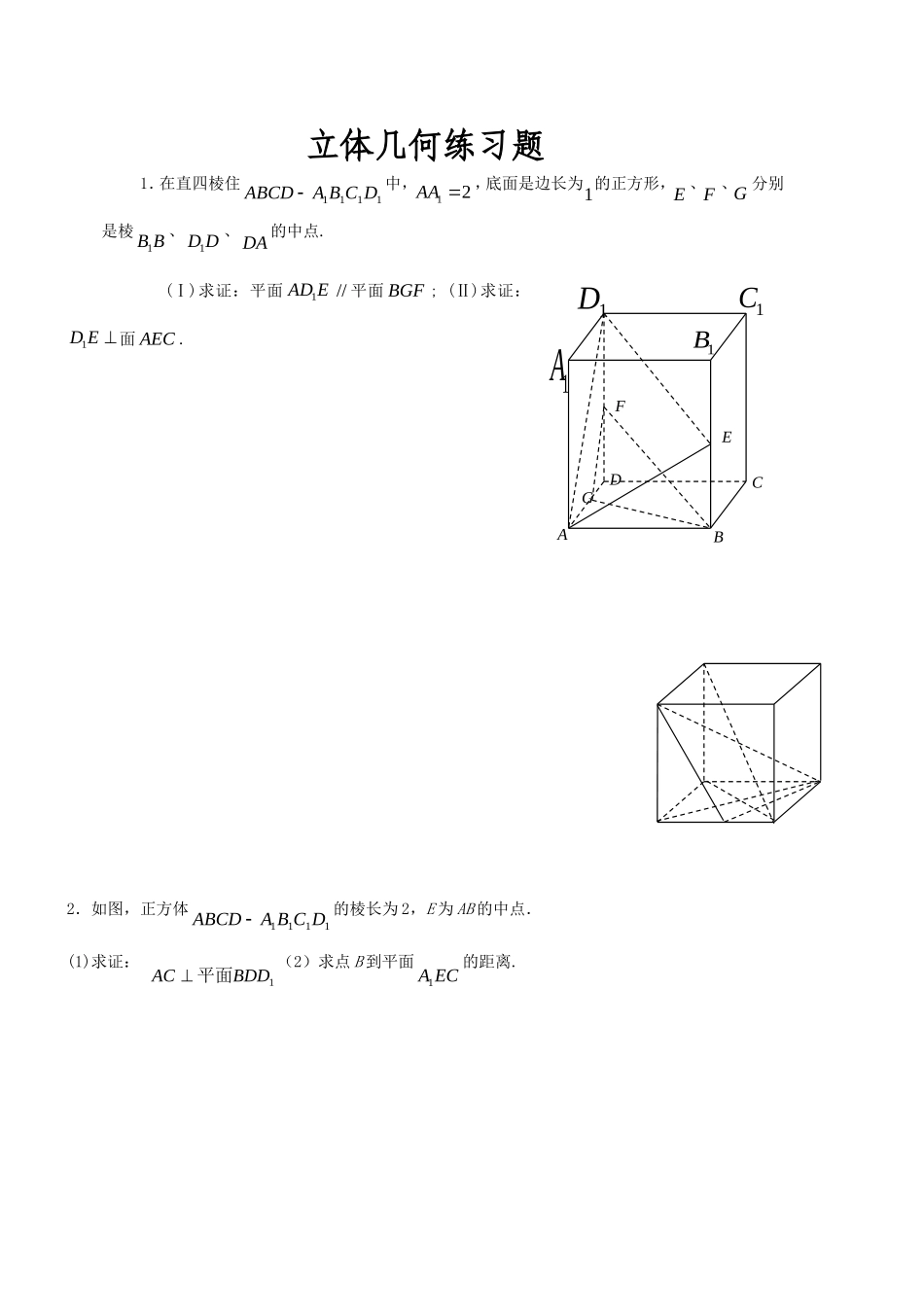
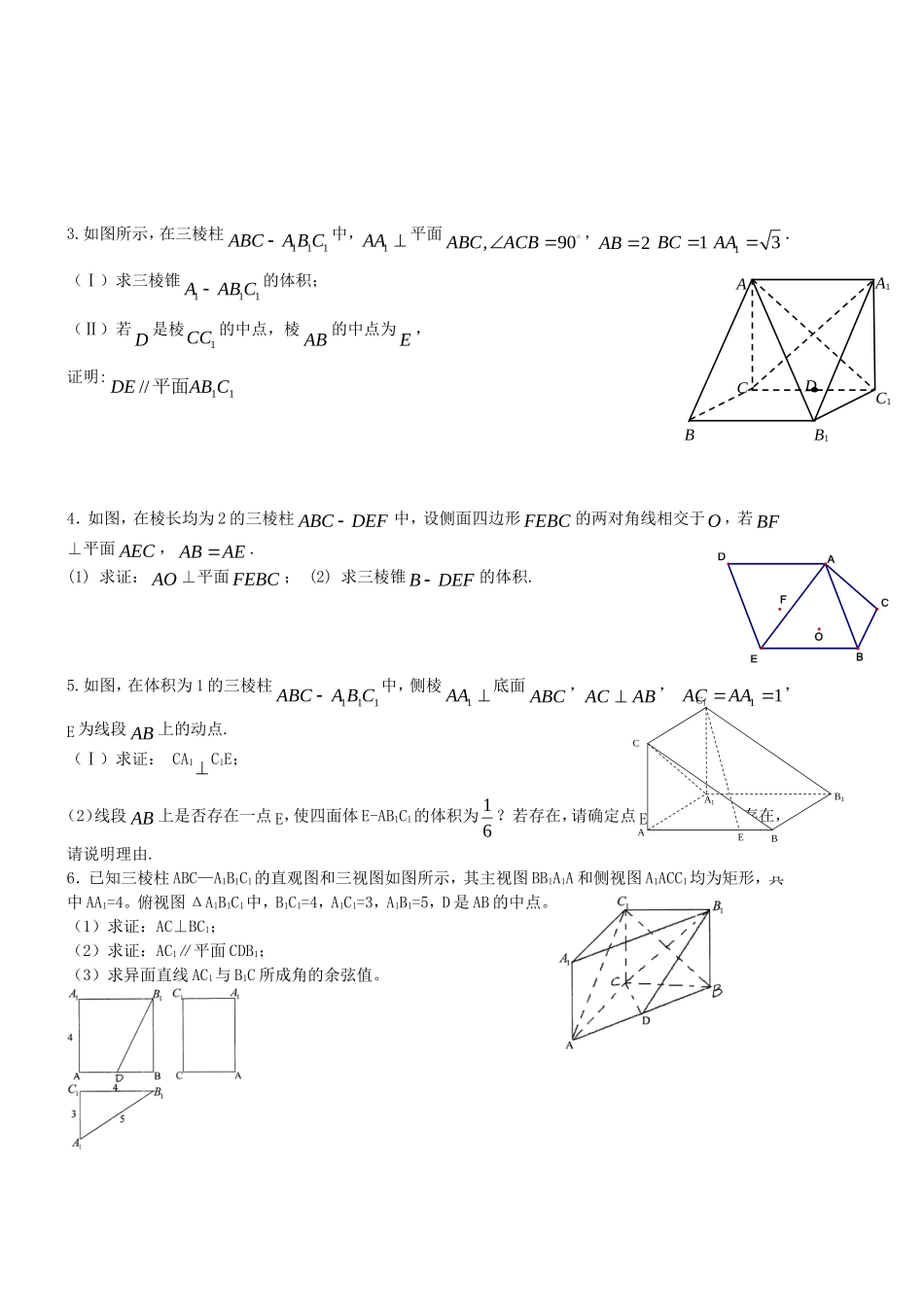
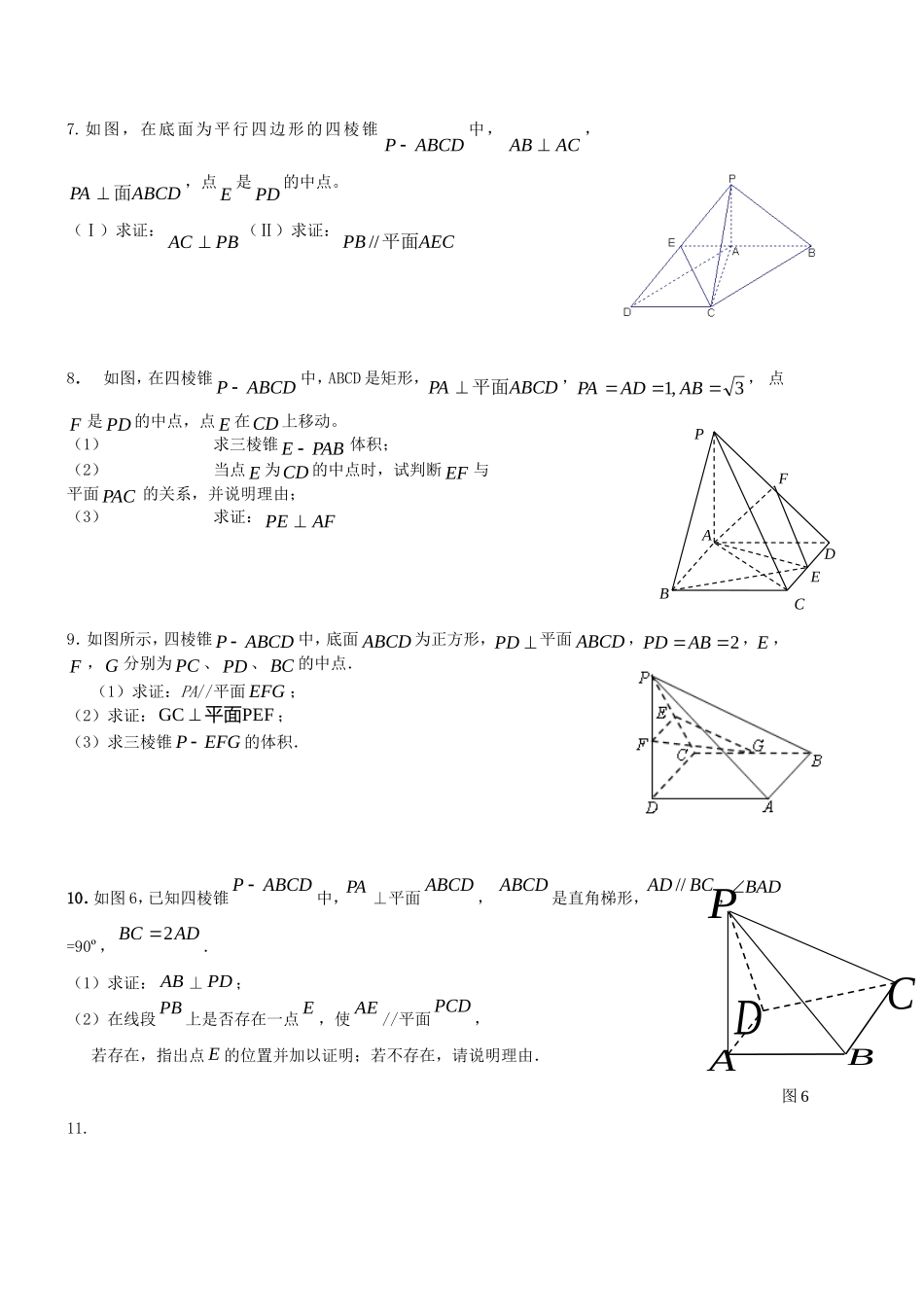
立体几何练习题1．在直四棱住1111DCBAABCD中，12AA，底面是边长为1的正方形，E、F、G分别是棱BB1、DD1、DA的中点.(Ⅰ)求证：平面EAD1//平面BGF;(Ⅱ)求证：1DE面AEC.2．如图，正方体1111DCBAABCD的棱长为2，E为AB的中点．(1)求证：1BDDAC平面（2）求点B到平面ECA1的距离.FEABDCG1C1A1B1DEOACBFD3.如图所示，在三棱柱111ABCABC中，1AA平面,90ABCACB，2AB1BC13AA．（Ⅰ）求三棱锥111AABC的体积；（Ⅱ）若D是棱1CC的中点，棱AB的中点为E，证明:11//CABDE平面4．如图，在棱长均为2的三棱柱ABCDEF中，设侧面四边形FEBC的两对角线相交于O，若BF⊥平面AEC，ABAE.(1)求证：AO⊥平面FEBC；(2)求三棱锥BDEF的体积.5.如图，在体积为1的三棱柱111CBAABC中，侧棱1AA底面ABC，ABAC，11AAAC，E为线段AB上的动点.（Ⅰ）求证：CA1PCCA11C1E；（2）线段AB上是否存在一点E，使四面体E-AB1C1的体积为61？若存在，请确定点E的位置；若不存在，请说明理由.6．已知三棱柱ABC—A1B1C1的直观图和三视图如图所示，其主视图BB1A1A和侧视图A1ACC1均为矩形，其中AA1=4。俯视图ΔA1B1C1中，B1C1=4，A1C1=3，A1B1=5，D是AB的中点。（1）求证：AC⊥BC1；（2）求证：AC1∥平面CDB1；（3）求异面直线AC1与B1C所成角的余弦值。ABCA1B1C1DBEC1A1CAB17.如图，在底面为平行四边形的四棱锥ABCDP中，ACAB，ABCDPA面，点E是PD的中点。（Ⅰ）求证：PBAC（Ⅱ）求证：AECPB平面//8．如图，在四棱锥ABCDP中，ABCD是矩形，ABCDPA平面，3,1ABADPA，点F是PD的中点，点E在CD上移动。（1）求三棱锥PABE体积；（2）当点E为CD的中点时，试判断EF与平面PAC的关系，并说明理由；（3）求证：AFPE9．如图所示，四棱锥PABCD中，底面ABCD为正方形，PD平面ABCD，2PDAB，E，F，G分别为PC、PD、BC的中点．（1）求证：PA//平面EFG；（2）求证：GCPEF平面；（3）求三棱锥PEFG的体积．10．如图6，已知四棱锥ABCDP中，PA⊥平面ABCD，ABCD是直角梯形，BCAD//，BAD=90º，ADBC2．（1）求证：AB⊥PD；（2）在线段PB上是否存在一点E，使AE//平面PCD，若存在，指出点E的位置并加以证明；若不存在，请说明理由．11.ACDBP图6ABCDPEFEAFCB图(1)E'AFCB图(2)..)2(;)1().2(,,,,,,,90,4,),1(的距离到平面求点求证如图上的射影恰为点在平面且位置到达使点折起将中点的分别是是等腰直角三角形如图BCAFCAEFEBCEFAAAAEFABACFEACBBCACABC12．如图所示是一个几何体的直观图、正视图、俯视图和侧视图C尺寸如图所示）。（Ⅰ）求四棱锥PABCD的体积；（Ⅱ）若GBC为上的动点，求证：AEPG。13．如图，四边形ABCD为矩形，DA平面ABE,2AEEBBC，BF平面ACE于点F，且点F在CE上.（Ⅰ）求证：AEBE；（Ⅱ）求三棱锥DAEC的体积；（Ⅲ）设点M在线段AB上，且满足2AMMB，试在线段CE上确定一点N，使得//MN平面DAE.14．已知四棱柱1111ABCDABCD的三视图如图所示.（1）画出此四棱柱的直观图，并求出四棱柱的体积；（2）若E为1AA上一点，//EB平面1ACD，AEBF·CD（19题图）M俯视图正视图侧视图22221BAAABDC1A1D1B1AD试确定E点位置，并证明EB平面11ABCD15.如图是以正方形ABCD为底面的正四棱柱被一平面所截得的几何体，四边形EFGH为截面，且ABADa，BFDHb．（Ⅰ）证明：截面四边形EFGH是菱形；（Ⅱ）求三棱锥FABH的体积．16．正方形ABCD中，AB=2，E是AB边的中点，F是BC边上一点，将△AED及△DCF折起(如下图)，使A、C点重合于A’点．(1)证明：A’DEF；(2)当BF=14BC时，求三棱锥A’一EFD的体积．17、已知四棱锥PABCD的三视图如下图所示，E是侧棱PC上的动点.(1)求四棱锥PABCD的体积；(2)是否不论点E在何位置，都有BDAE？证明你的结论；(3)若点E为PC的中点，求二面角DAEB的大小.18、如图，已知AB平面ACD，DE平面ACD，△ACD为等边三角形，2ADDEAB，F为CD的中点.(1)求证：//AF平面BCE；(2)求证：平面BCE平面CDE；(3)求直线BF和平面BCE所成角的正弦值.GFCADBHE俯视图侧视图正视图121121ABCDPEABCDEF19、如图，四棱锥P—ABCD中，底...