连续介质力学第二章VIP免费

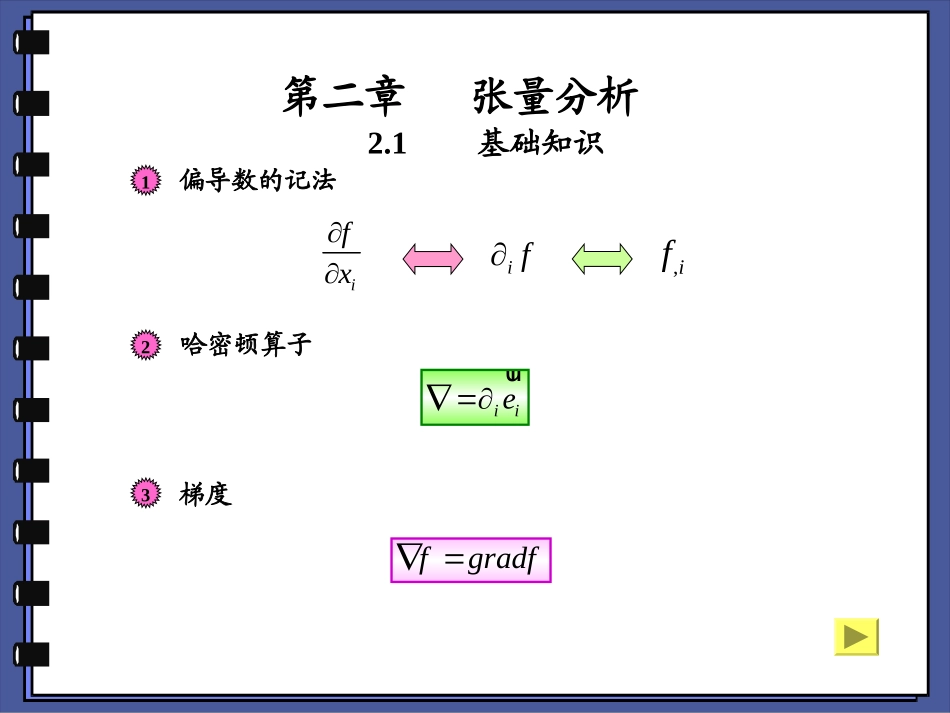
第二章张量分析ifxif,if偏导数的记法12哈密顿算子iieur3梯度fgradf2.1基础知识则梯度为：ffffijkxyzrrr标量的梯度：标量函数：()ffrr展开后有：112233fefefeururur原式iigradfefur()()iijjgradaaeaerrurur()()iijjeaeurur()()ijijaeeurur矢量的梯度：yxzyxzyxzaaaxxxaaayyyaaazzz左梯度aaradgjjiiaee,ijijaeejiijeeajiijxaa其中：iijjaxee右梯度两者关系()Taa左梯度右梯度332313322212312111xaxaxaxaxaxaxaxaxaa写成矩阵形式为：张量的梯度：ijkijkTeeeiijkjkTeee设T为任意二阶张量它的左梯度gradT定义为：TgradTT的右梯度定义为：jkjkiiTeeegradTTijkjkiTeeeTT一般地4散度矢量场的散度矢量场的左散度定义为：divaarr112233aaayxzaaaxyzijijaiia()()iijjeaeurur原式右散度表示为：aaivdaaivdjjiiaeeiiiiijijaxaxa332211xaxaxaaaivddiv显然今后对于矢量场的左散度和右散度不加区别()()kkijijdiveTeeTTurururiijjTeur112233iiiiiiTeTeTeururur张量的散度kijkijTeurTTdiv关于二阶张量场的左散度定义为：PTT1132233333()TTTeur()()xxyxzxxyyyzyTTTiTTTjxyzxyzrr()xzyzzzTTTkxyzr展开后有：11122133111122223322()()TTTeTTTeurur原式关于二阶张量场的右散度定义为：PTTTTivdTTivdjjikkiTeeekjkiijxTekikixTeikikTeTTivddiv一般地，，当T为对称张量的时候，两者相等5旋度curlaa()()kkiieae�112233()()()kikikikikikieaeeaeeae�原式展开后有：123123123xxxaaaeeekijkijeae�＝矢量场的旋度：左旋度：231233213211321331232()()ieaeaeeaeae�12312213213()eaeae�233213113212213()()()aaeaaeaae�yyxxzzaaaaaayzzxxy（-）i（-）j（-）k右旋度：iijjaurlceeaaijijxaeekijjikxaeeijkijkeaea.张量场的旋度设T为任意二阶张量，则它的左旋度定义为：TTcurlkiikjjTeeekpikjjipTeeekppkeeTikjjippkTeT其中：右旋度定义为：TTurlcjjkiikTeeekiikjkjpTeeepiipeeTikjkjpipTeT其中：小结：iieur哈密顿算子梯度iigradffefur散度iidivaaarr旋度curlaa2ffiif展开后有：()()iijjefe�原式()ijijf112233fff222222fffxyz2.2Laplace算子公式：2.3物质导数ffxfyfztxtytzt123()()()fxyzfffttttiixffttiifVftfVft�(,())fftrt若DfffrDttrt则：()()()DVDtt�2.4积分定理1Gauss定理(coscoscos)()SVPQRPQRrdsdxdydzxyz3r�1r�2r�1dS2dS3dS有向面积：123231312dSdrdrdSdrdrdSdrdr���()aP、Q、R根据Gauss定理有：左边112233()SananandSiiSandSSandSSadS��右边112233()VaaadViiVadVVadVSVadSadV��2Stokes定理[(...