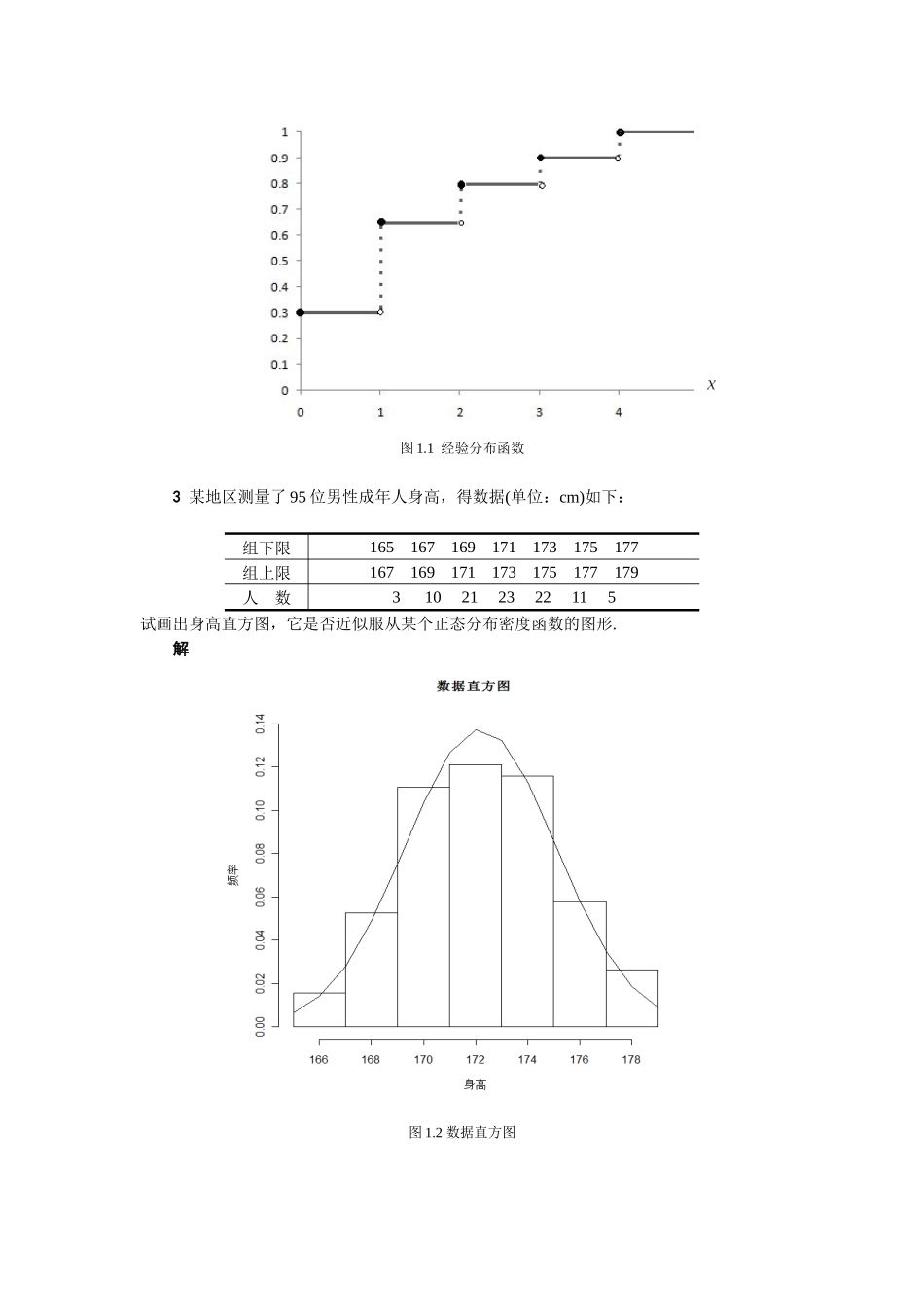
习题一1设总体X的样本容量n=5,写出在下列4种情况下样本的联合概率分布.1)X~B(1,p);2)X~P(λ);3)X~U[a,b];4)X~N(μ,1).解设总体的样本为,1)对总体,其中:2)对总体其中:3)对总体4)对总体2为了研究玻璃产品在集装箱托运过程中的损坏情况,现随机抽取20个集装箱检查其产品损坏的件数,记录结果为:1,1,1,1,2,0,0,1,3,1,0,0,2,4,0,3,1,4,0,2,写出样本频率分布、经验分布函数并画出图形.解设代表各箱检查中抽到的产品损坏件数,由题意可统计出如下的样本频率分布表1.1:表1.1频率分布表i01234个数673220.30.350.150.10.1经验分布函数的定义式为:,据此得出样本分布函数:图1.1经验分布函数3某地区测量了95位男性成年人身高,得数据(单位:cm)如下:组下限165167169171173175177组上限167169171173175177179人数310212322115试画出身高直方图,它是否近似服从某个正态分布密度函数的图形.解图1.2数据直方图它近似服从均值为172,方差为5.64的正态分布,即.4设总体X的方差为4,均值为μ,现抽取容量为100的样本,试确定常数k,使得满足P(|¯X−μ|c)=0.1.解易知,则;同理,则又因:,所以与相互独立.所以:计算得:c=0.976.17设为总体的容量的样本,为样本的样本均值和样本方差,求证:1);2);3).解1)因:,所以:,又:且:与相互独立所以:~2)由1)可得:3)因:,所以:18设为总体的样本,为样本均值,求,使得.解所以:查表可得:,即.19设为总体的样本,试求:1)的密度函数;2)的密度函数;解因:,所以的密度函数为:,由定理:20设为总体的样本,试求:1);2)解21设为总体的一个样本,试确定下列统计量的分布:1);2);3)Y3=1mσ2(∑i=1mXi)2+1nσ2(∑i=m+1m+nXi)2解1)因为:所以:,且与相互独立,由抽样定理可得:2)因为:,且与相互独立,所以:3)因为:,所以:,且与相互独立,由卡方分布可加性得:.22设总体X服从正态分布N(μ,σ2),样本X1,X2,⋯,Xn来自总体X,S2是样本方差,问样本容量n取多大能满足P((n−1)S2σ2≤32.67)=0.95?解由抽样分布定理:,,查表可得:,.23从两个正态总体中分别抽取容量为20和15的两独立的样本,设总体方差相等,S12,S22分别为两样本方差,求P(S12S22>2.39).解设分别为两样本的容量,为总体方差,由题意,又因S12,S22分别为两独立的样本方差:所以:.24设总体X~N(μ,σ2),抽取容量为20的样本X1,X2,⋯,X20,求概率1)P(10.85≤∑i=120(Xi−μ)2σ2≤37.57);2)P(11.65≤∑i=120(Xi−¯X)2σ2≤38.58).解1)因,且各样...