运筹学例题及答案VIP免费

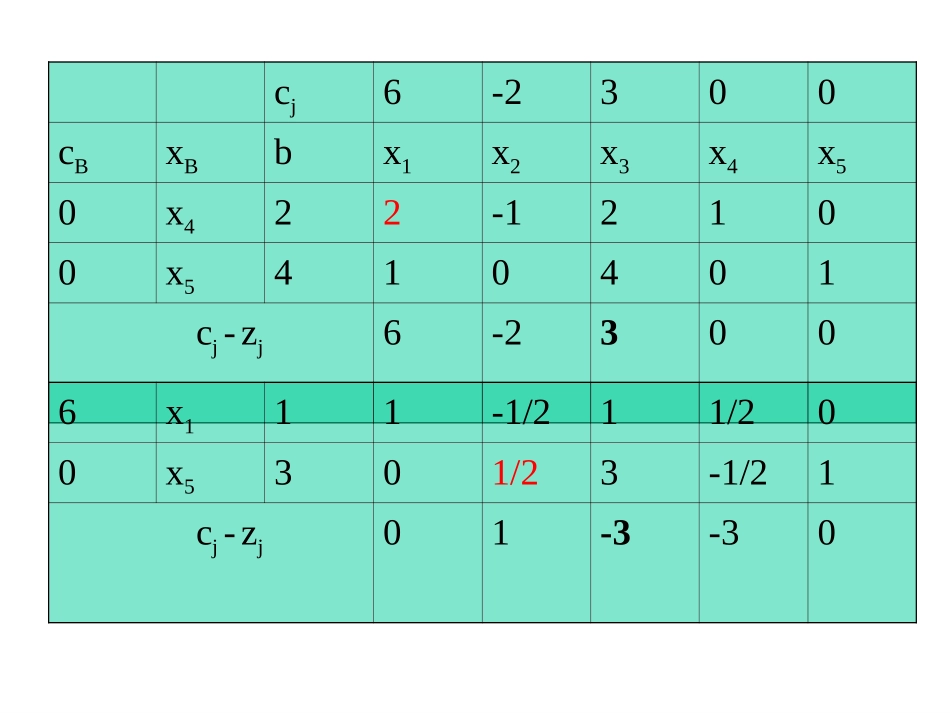
运筹帷幄之中决胜千里之外作业及答案11。用单纯形法解。用单纯形法解LPLP问题问题0,,44222..326max32131321321xxxxxxxxtsxxxz线性规划cj6-2300cBxBbx1x2x3x4x50x422-12100x5410401cj-zj6-23006x111-1/211/200x5301/23-1/21cj-zj01-3-306x1410401-2x26016-12cj-zj00-9-2-2cj6-2300cBxBbx1x2x3x4x5达到最优解，且最优解唯一22。用大。用大MM或两阶段法解或两阶段法解LPLP问题问题0,,02226..22max3213231321321xxxxxxxxxxtsxxxzcj2-12000-M-M-McBxBbx1x2x3x4x5x6x7x8x9-Mx76111-100100-Mx82-2010-10010-Mx9002-100-1001Cj-zj2-M3M-1M+2-M-M-M000-Mx76103/2-101/210-1/2-Mx82-2010-10010-1x2001-1/200-1/2001/2Cj-zj2-M05/2M+3/2-M-M1/2M-1/200-3/2M+1/2cj2-12000-M-M-McBxBbx1x2x3x4x5x6x7x8x9-Mx73400-13/21/21-3/2-1/22x32-201000010-1x21-1100-1/2-1/201/21Cj-zj5+4M00-M3/2M+3/21/2M-1/20-5/2M-3/2-3/2M+1/22x13/4100-1/43/81/81/4-3/8-1/82x37/2001-1/2-1/41/41/21/4-1/4-1x27/4010-1/4-1/8-3/81/81/83/8Cj-zj0005/4-----无界解3，某厂在今后四个月内需租用仓库堆放物资。已知各月份需租用仓库面积见表，仓库租借费用随合同期不同而不同，期限越长折扣越大，具体数字见表。租借合同每个月月初都可办理，合同规定具体的租借面积和月数，因此该厂可根据需要，在任何一个月月初办理合同，每次办理可签一份或多份，总目标是总的租借费用最低，请建立数学模型并用软件给出结果。月份1234所需仓库面积（100m2）15102012合同租借期限1个月2个月3个月4个月租借费用2800450060007300解:设一月初签订合同期限为一个月，两个月，三个月，四个月的仓库面积分别为，，，，二月初签订合同期限为一个月，两个月，三个月的仓库面积分别为，三月初签订合同期限为一个月，两个月的仓库面积分别为，四月初签订合同期限为一个月的仓库面积为。则11x12x13x14x232221,,xxx3231,xx41x142313322212413121117300)(6000)(4500)(2800minxxxxxxxxxxz0122010154132231432312322141323222114131214131211ijxxxxxxxxxxxxxxxxxxxxx计算结果如下4，某厂生产I,II,III三种产品，都分别经过A,B两道工序加工。设A工序可分别在设备A1或A2上完成，有B1，B2，B3三种设备可用于完成B工序。已知产品I可在A,B任何一种设备上加工；产品II可在任何规格的A设备上加工，但完成B工序时，只能在B1设备上加工；产品III只能在A2和B2设备上加工。加工单位产品所需的工序时间及其它各项数据见表，试安排最优生成计划，使该厂获利最大。设备产品IIIIII设备有效台时设备加工费（元/h）A151060000.05A27912100000.03B16840000.06B241170000.11B3740000.05原料费（元/件）售价（元/件）0.250.350.501.252.002.80解：设第Ⅰ种产品中，分别在上加工的数量依次为，第Ⅱ种产品中分别在A1,B1和A2,B1上加工的数量为生产Ⅲ种产品数量为。3,2,1),,(),,(21jBABAjj654321,,;,,xxxxxx87,xx9x04000)(7700011)(44000)(8)(610000129)(7600010)(5)(705.0]11)(4[11.0)](8)(6[06.0]129)(7[03.0]10)(5[05.0)5.08.2())(35.02())(25.025.1(max639528741986547321639528741986547321987654321jxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxz对偶理论1.已知线性规划问题：0,,,966283..42max4321321432214214321xxxxxxxxxxxxxxxtsxxxxz要求：a)写出对偶问题，b)已知原问题最有解X*=(2,2,4,0),用互补松弛性求出对偶问题的最优解。解：对偶问题：0,,,114322..9668min4321314343214214321yyyyyyyyyyyyyyytsyyyyw将原问题的最优解带入约束，发现第4个约束为严格不等式，所以，得y4*=0又因为，原问题最优解的前三个分量都大于0，所以，有如下三个等式成立。...