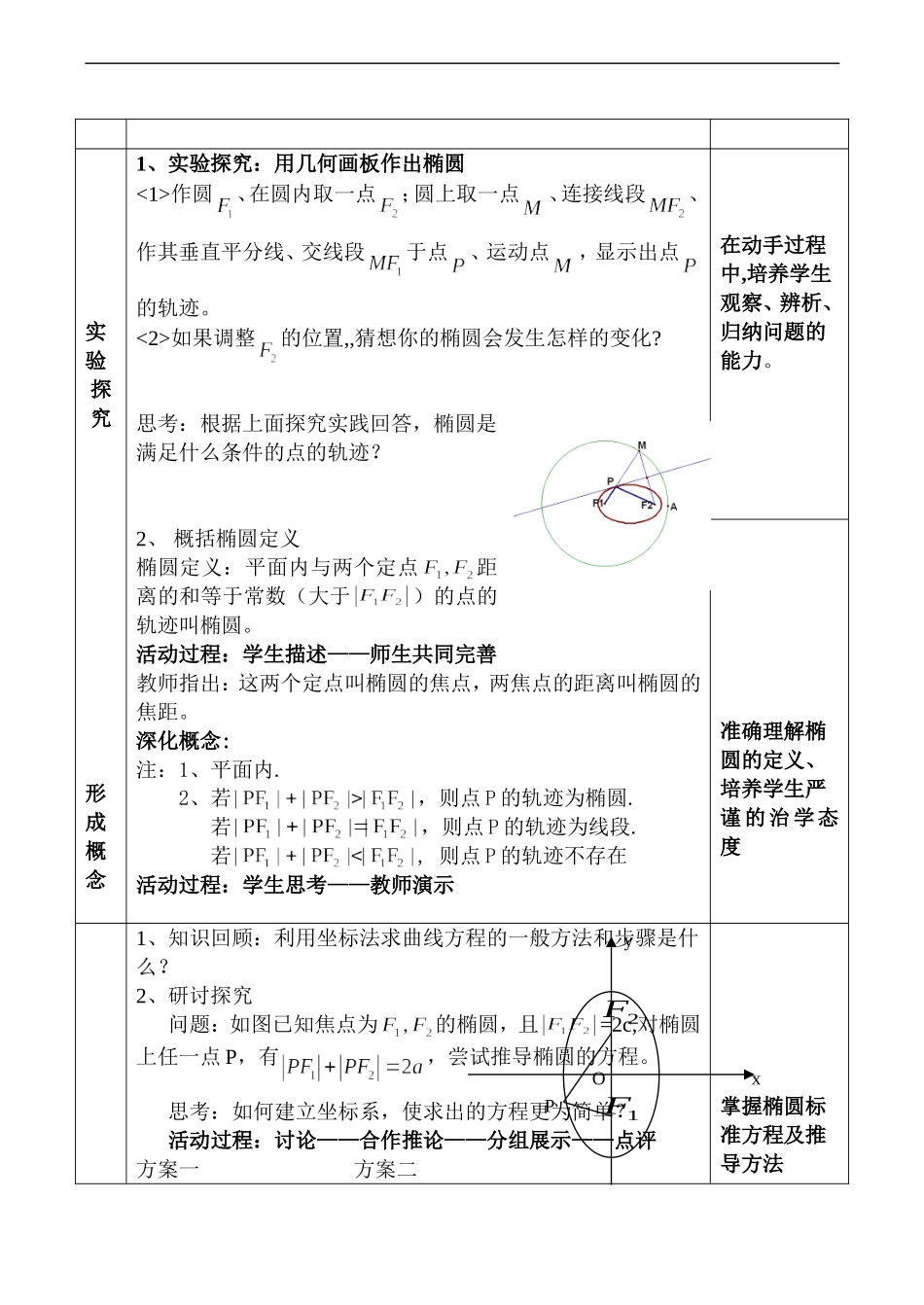
高二数学椭圆及其标准方程教材:人教社《全日制普通高级中学教科书》(试验修订本•必修)数学•第二册(上)一、教学目标根据教学大纲要求和学生身理、心理结构及我校学生特点,通过学生学习,学生应该达到以下要示。(1)知识与能力目标:学习椭圆的定义,掌握椭圆标准方程的两种形式及其推导过程;能根据条件确定椭圆的标准方程,掌握用待定系数法求椭圆的标准方程。(2)过程与方法目标:通过对椭圆概念的引入教学,培养学生的观察能力和探索能力;通过对椭圆标准方程的推导,使学生进一步掌握求曲线方程的一般方法,提高学生运用坐标法解决几何问题的能力,并渗透数形结合和等价转化的数学思想方法。(3)情感、态度与价值观目标:通过让学生大胆探索椭圆的定义和标准方程,激发学生学习数学的积极性,培养学生勇于探索的精神和渗透辩证唯物主义的方法论和认识论。通过经历椭圆方程的化简,增强学生战胜困难的意志品质并体会数学的简洁美、对称美.通过讨论椭圆方程推导的等价性养成学生扎实严谨的科学态度.二、教学重点、难点(1)教学重点:椭圆的定义及椭圆标准方程。(2)教学难点:椭圆标准方程的建立和推导。三:教学媒介多媒体、实物投影、《几何画板》四、教学过程:教学环节教学内容和形式设计意图创设情境引入概念1、动画演示嫦娥一号绕月飞行的图像、相关月球图片和神州五号绕月飞行图。(背景音乐《月亮之上》)2、数学实验演示:用几何画板演示椭圆。3、思考:椭圆是满足什么条件的点的轨迹呢?培养学生的爱国主义精神、探求科学的激情。培养学生的归纳的能力。实验探究形成概念1、实验探究:用几何画板作出椭圆<1>作圆、在圆内取一点;圆上取一点、连接线段、作其垂直平分线、交线段于点、运动点,显示出点的轨迹。<2>如果调整的位置,,猜想你的椭圆会发生怎样的变化?思考:根据上面探究实践回答,椭圆是满足什么条件的点的轨迹?2、概括椭圆定义椭圆定义:平面内与两个定点距离的和等于常数(大于)的点的轨迹叫椭圆。活动过程:学生描述——师生共同完善教师指出:这两个定点叫椭圆的焦点,两焦点的距离叫椭圆的焦距。深化概念:注:1、平面内.2、若,则点P的轨迹为椭圆.若,则点P的轨迹为线段.若,则点P的轨迹不存在活动过程:学生思考——教师演示在动手过程中,培养学生观察、辨析、归纳问题的能力。准确理解椭圆的定义、培养学生严谨的治学态度1、知识回顾:利用坐标法求曲线方程的一般方法和步骤是什么?2、研讨探究问题:如图已知焦点为的椭圆,且=2c,对椭圆上任一点P,有,尝试推导椭圆的方程。思考:如何建立坐标系,使求出的方程更为简单?活动过程:讨论——合作推论——分组展示——点评方案一方案二掌握椭圆标准方程及推导方法xy1F2FPO研讨探究推导方程按方案一建立坐标系,师生研讨探究得到椭圆标准方程+=1(),其中b2=a2-c2(b>0);选定方案二建立坐标系,由学生完成方程化简过程,可得出+=1,同样也有a2-c2=b2(b>0)。培养学生战胜困难的意志品质并感受数学的简洁美、对称美.归纳概括方程特征观察椭圆图形及其标准方程,师生共同总结归纳(1)椭圆标准方程对应的椭圆中心在原点,以焦点所在轴为坐标轴;(2)椭圆标准方程形式:左边是两个分式的平方和,右边是1;(3)椭圆标准方程中三个参数a,b,c关系:;培养学生观察归纳能力应用举例例1、求适合下列条件的椭圆的标准方程(1)两个焦点的坐标分别是,椭圆上一点P到两焦点距离和等于10。(2)两焦点坐标分别是,并且椭圆经过点。(3)。活动过程:分析——解答(板演)——点评变式练习:运用椭圆的定义,掌握椭圆的标准方程.xy1F2FPO1.如果椭圆上一点P到焦点的距离等于6,则P到另一个焦点的距离为。2、椭圆一个焦点是(0,-4)则=。3、经过、的椭圆的方程为。教师活动:组织------发现问题------个别辅导-----点评学生活动:分析-----解答------展示------交流变式提高深化概念课堂小结提问:本节课学习的主要知识是什么?你学会了哪些数学思想与方法?活动过程:教师提问-----学生小结-----师生补充完善让学生回顾本节所学知识与方法,以逐步提高学生自我获取知识的能力作业布置1:教材第95页,练习...