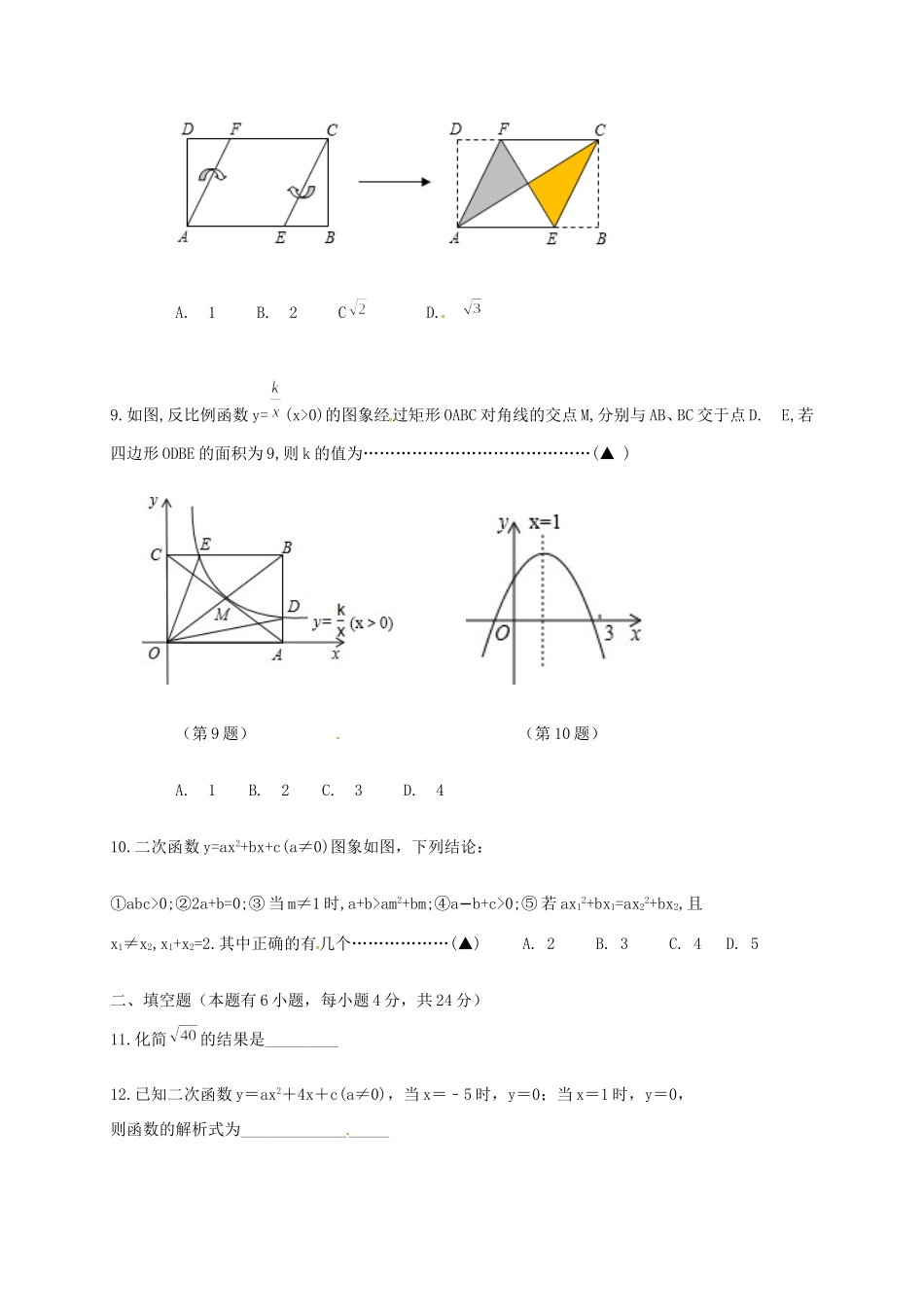
九年级数学暑假作业检测一、选择题(本题有10小题,每小题3分,共30分)1.如果1≤a≤,则+|a-2|的值是………………………………(▲)A.6+aB.-6-aC.-aD.12.若一元二次方程有一个根为0,则m的值为(▲)A.m=1B.m=-1C.m=D.以上结论都不对。3.下列一元二次方程两实数根的和为-4的是…………………………………………(▲)A.B.C.D.4.已知.则的值为……………………………………(▲)A.-2B.+2C.D.5.在同一坐标平面内,图象不可能由函数y=2x2+1的图象通过平移变换、轴对称变换得到的函数是…………………………………………………………………………………………(▲)A.y=2(x+1)21B.−y=2x2+3C.y=2x−21D.−6.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是…………………………………………………(▲)A.(3+x)(40.5x)=15B.(x+3)(4+0.5x)=15C.(x+4)(30.5x)=15D.(x+1)−−(40.5x)=15−7.已知抛物线y=a(x1)−2+k(a,k是常数,且a>0)上三点P1(2,y−1),P2(1,y−2),P3(2,y3),则……………………………………………………………………………………………(▲)A.y1>y2>y3B.y3>y2>y1C.y3>y1>y2D.y2>y1>y38.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为(▲)A.1B.2CD.9.如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D.E,若四边形ODBE的面积为9,则k的值为……………………………………(▲)(第9题)(第10题)A.1B.2C.3D.410.二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④ab+c>0;−⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有几个………………(▲)A.2B.3C.4D.5二、填空题(本题有6小题,每小题4分,共24分)11.化简的结果是_________12.已知二次函数y=ax2+4x+c(a≠0),当x=﹣5时,y=0;当x=1时,y=0,则函数的解析式为__________________13.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是______________.14._________15.如图,正方形ABCD的边长是4,的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值_____________。(第15题)(第16题)16.如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=(x>0)的图象上,顶点A1、B1分别在x轴和y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=(x>0)的图象上,顶点A2在x轴的正半轴上,则P2点的坐标为________P3的坐标为_________.三、解答题(本题有8小题,共66分)17.计算(本题6分)(2)18.解方程(本题6分)(1)(2)19.(本题6分)如图,P是正方形ABCD对角线BD上的一点,PE⊥DC,PF⊥BC,垂足分别为E,F.求证:AP=EF.20.(本题8分)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:根据以上信息,整理分析数据如下:(1)写出表格中a=_______b=_______,(2)求出c的值;21.(本题8分)在直角坐标系中,已知反比例函数图象经过点D(5,1),且轴,垂足为B,点C是第三象限图象上的动点,过C作轴,垂足为A,连接AB,BC.(1)求k的值;(2)若的面积是10,求直线CD解析式;22.(本题10分)如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.(1)求m的值及这个二次函数的关系式;(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为a,求h与a之间的函数关系式,并写出自变量a的取值范围;(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.23.(本题10分)已知四边形ABCD是菱形,AB=4,,的两边分别与射线CB、DC相交于点E、F,且。(1)如图1所示,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系。(2)如图2所示,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF。(3)如图3所示,当点E在线段CB的延长线上,且时,求点F到BC的距离。(提示过点F做)24.(本题12分)如图,在平面直角坐标系xOy中,已知直线分别交反比例函数和在第一象限的图象于点A,B,过点B作轴于点D,交的图象于点C,连结AC.(1)若点B的横坐标为2,求点A的坐标(2)若是等腰三角形,求k的值是多少?