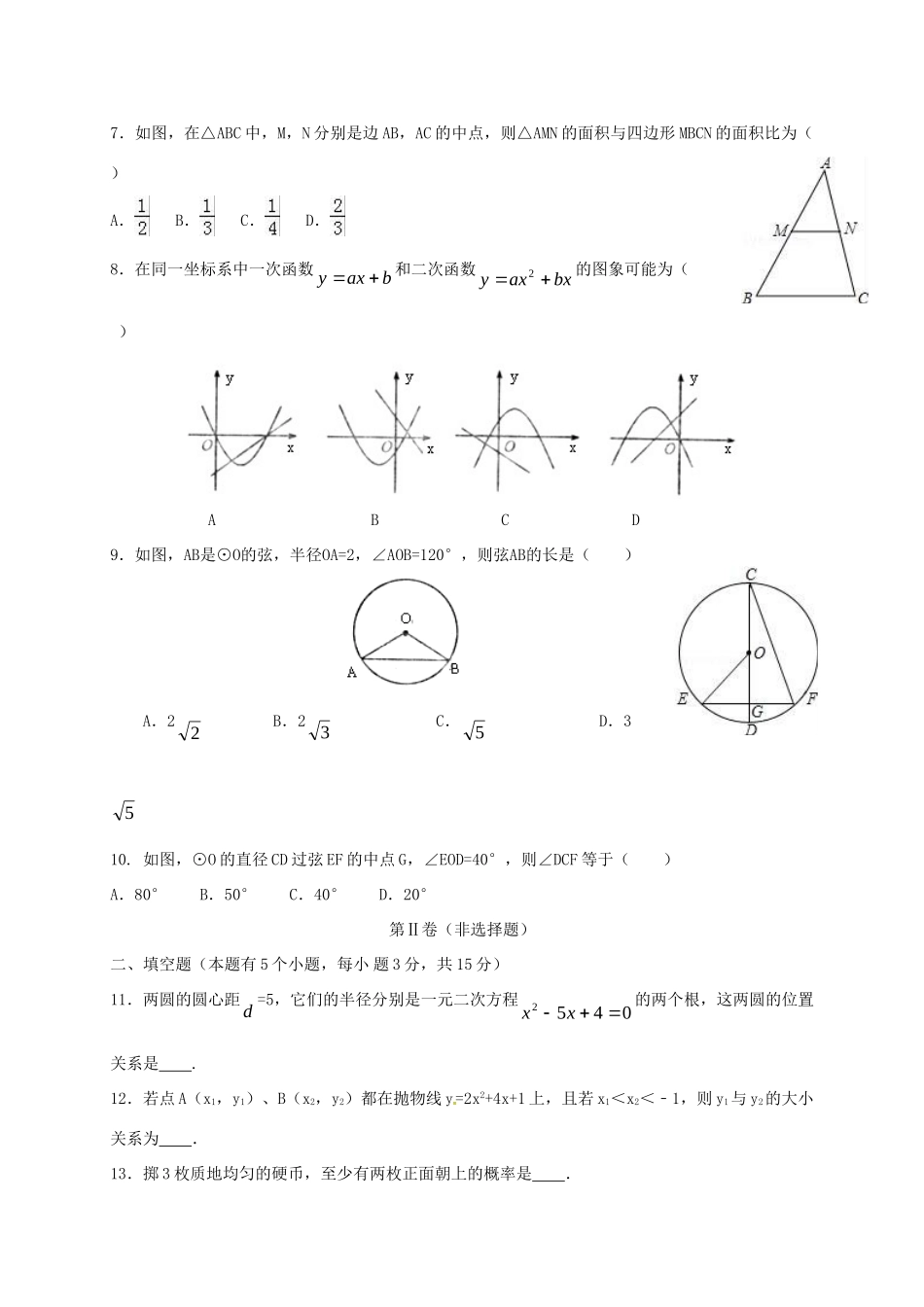
山东省曲阜市2018届九年级数学上学期期末试题注意事项:本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷为选择题,30分,第Ⅱ卷为非选择题,70分;共100分,考试时间为120分钟.第Ⅰ卷(选择题共30分)一、选择题(在每小题给出的四个选项中,只有一个是正确的,每小题3分,共30分).1.方程x(x﹣2)=x﹣2的根是()A.x=1B.x1=1,x2=2C.x1=2,x2=0D.x=22.下列各图是选择自历届世博会会徽中的图案,其中是中心对称图形的是()ABCD3.下列事件中,必然事件是()A.掷一枚硬币,正面朝上B.a是实数,0||aC.某运动员跳高的最好成绩是20.1米D.从车间刚生产的产品中任意抽取一个,是次品4.下列关于函数y=(x﹣6)2+3的图象,下列叙述错误的是()A.图象是抛物线,开口向上B.对称轴为直线x=6C.顶点是图象的最高点,坐标为(6,3)D.当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大5.如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为()A.(0,)B.(0,﹣3)C.(﹣1,0)D.(3,0)6.双曲线y=位于第二、第四象限,则下面说法正确的是()A.y随x的增大而增大B.y随x的增大而减小C.k>0D.k<07.如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为()A.B.C.D.8.在同一坐标系中一次函数baxy和二次函数bxaxy2的图象可能为()ABCD9.如图,AB是⊙O的弦,半径OA=2,∠AOB=120°,则弦AB的长是()A.22B.23C.5D.3510.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于()A.80°B.50°C.40°D.20°第Ⅱ卷(非选择题)二、填空题(本题有5个小题,每小题3分,共15分)11.两圆的圆心距d=5,它们的半径分别是一元二次方程0452xx的两个根,这两圆的位置关系是.12.若点A(x1,y1)、B(x2,y2)都在抛物线y=2x2+4x+1上,且若x1<x2<﹣1,则y1与y2的大小关系为.13.掷3枚质地均匀的硬币,至少有两枚正面朝上的概率是.14.如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为.15.如图,在Rt△ABC中,∠C=90°,∠B=58°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为.三、解答题(共55分,请把答案填写在答题纸指定的位置上)16.解方程:(每题3分,共6分)(1)x2﹣4x﹣5=0(2)104)52(xxx.17.(本题满分6分)在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.18.(本题满分7分)把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.(1)请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.19.(本题满分9分)如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、日的坐标分别为A(-2,3)、B(-3,1).(1)画出△AOB绕点O顺时针旋转90°后的△A1OB1;(2)写出点A1的坐标;(3)求点A旋转到A1所经过的路线长.20.(本题满分9分)已知:△ABC内接于⊙O,过点A作直线EF.学校班级姓名考号.(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况):①;②;③.(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因21.(本题满分8分)已知正比例函数y=kx(k≠0)与反比例函数y=的图象都过点A(m,1).(1)求此正比例函数解析式;(2)求这两个函数图象的另一个交点坐标.22.(本题满分l0分)抛物线abxaxy32经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求此抛物线的解析式;(2)已知点D(m,1m)在第四象限的抛物线上,求点D关于直线BC对称的点的坐标;(3)在(2)的条件下,连结BD,问在x轴上是否存在点P,使∠PCB=∠CBD,若存在,请求出P点的坐标;若不存在,请说明理由.