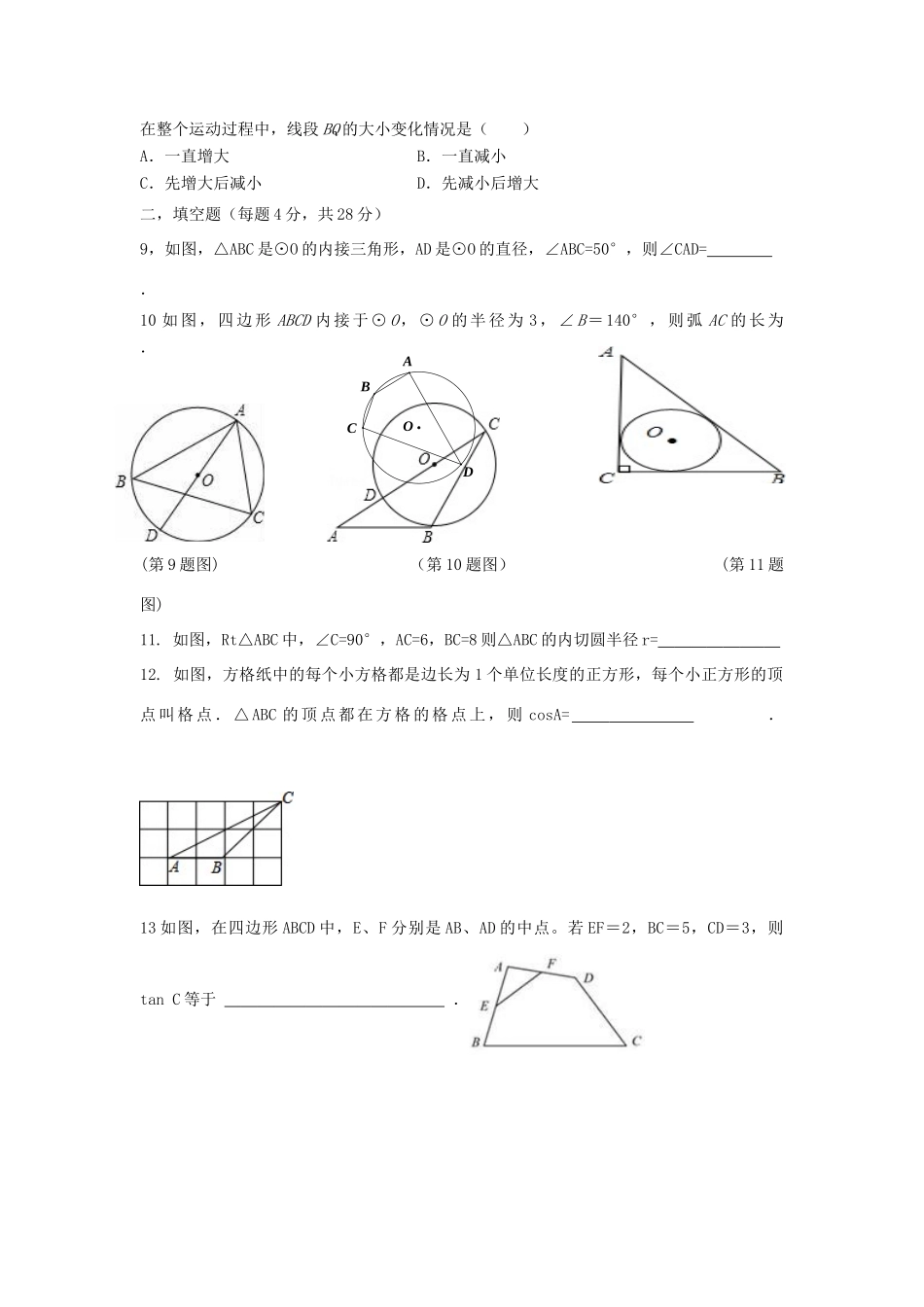
浙江省乐清育英学校初中分校2017-2018学年八年级数学下学期期中试题一,选择题(每题4分,共32分)1.由5个相同的正方体组成的几何体如图所示,则它的主视图是()A.B.C.D.2在△ABC中,若cosA=,tanB=,则这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形3.如图所示的是某几何体的三视图,则该几何体的形状是()A.三棱锥B.正方体C.三棱柱D.长方体4如图,AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C度数为(.)A.60°C.40°D.72°D、60°或120°5个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么tanθ的值是()A.B.C.D.(5题图)(6题图)(8题图)6如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是()A.30°B.45°C.60°D.40°7已知等腰三角形的三边长为a、b、c,且ca,若关于x的一元二次方程022cbxx的两根之差为2,则等腰三角形的一个底角是()A.15°B.30°C.45°D.60°8如图,在△ABC中,∠ACB=90°.P是BC边上一动点,以PC为直径作⊙O,连结AP交⊙O于点Q,连结BQ,点P从点B出发,沿BC方向运动,当点P到达点C时,点P停止运动.QPABCO在整个运动过程中,线段BQ的大小变化情况是()A.一直增大B.一直减小C.先增大后减小D.先减小后增大二,填空题(每题4分,共28分)9,如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD=.10如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为.(第9题图)(第10题图)(第11题图)11.如图,Rt△ABC中,∠C=90°,AC=6,BC=8则△ABC的内切圆半径r=12.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA=.13如图,在四边形ABCD中,E、F分别是AB、AD的中点。若EF=2,BC=5,CD=3,则tanC等于.ODCAB14如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.15已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.如果AC=3,则PD的长为三,解答题16,(4分)28)14.3(45sin20;17(5分),小芳想测树高.她将一根细线固定在半圆形量角器的圆心处,细线的别一端系一个小重物,制成了一个简单的测角仪(如图1);将此测角仪拿在眼前,使视线沿着仪器的直径刚好到达树的最高点(如图3);测得∠ABC=60°,小芳眼睛离地1.5米,量得小芳到树根的距离是5米,则树高多少?18(9分).如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).(1)把△ABC沿BA方向平移后,点A移到点1A,在网格中画出平移后的△111CBA;(2)把△111CBA绕点1A按逆时针旋转90,在网格(第17题图1)(第17题图2)(第17题图3)ABC1A(第18题)中画出旋转后的△221CBA;(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.19.(本题10分)如图,在△ABC中,∠C=90,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.(1)求证:∠EDB=∠B.(2)若sinB=35,AB=10,OA=2,求线段DE的长.20.(本题10分)如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.(1)求证:AD=CE.(2)若DE=3,CE=4,求tan∠DAE的值.21(本题10分)如图,以O为圆心的弧度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.(1)求的值;(2)若OE与交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;(3)在(2)的条件下,若BC=1,求tan∠BCO的值.22(本题12分.)如图1,已知点A(8,4),点B(0,4),线段CD的长为3,点C与原点O重合,点D在x轴正半轴上.线段CD沿x轴正方向以每秒1个单位长度的速度向右平移,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F(如图2),设运...