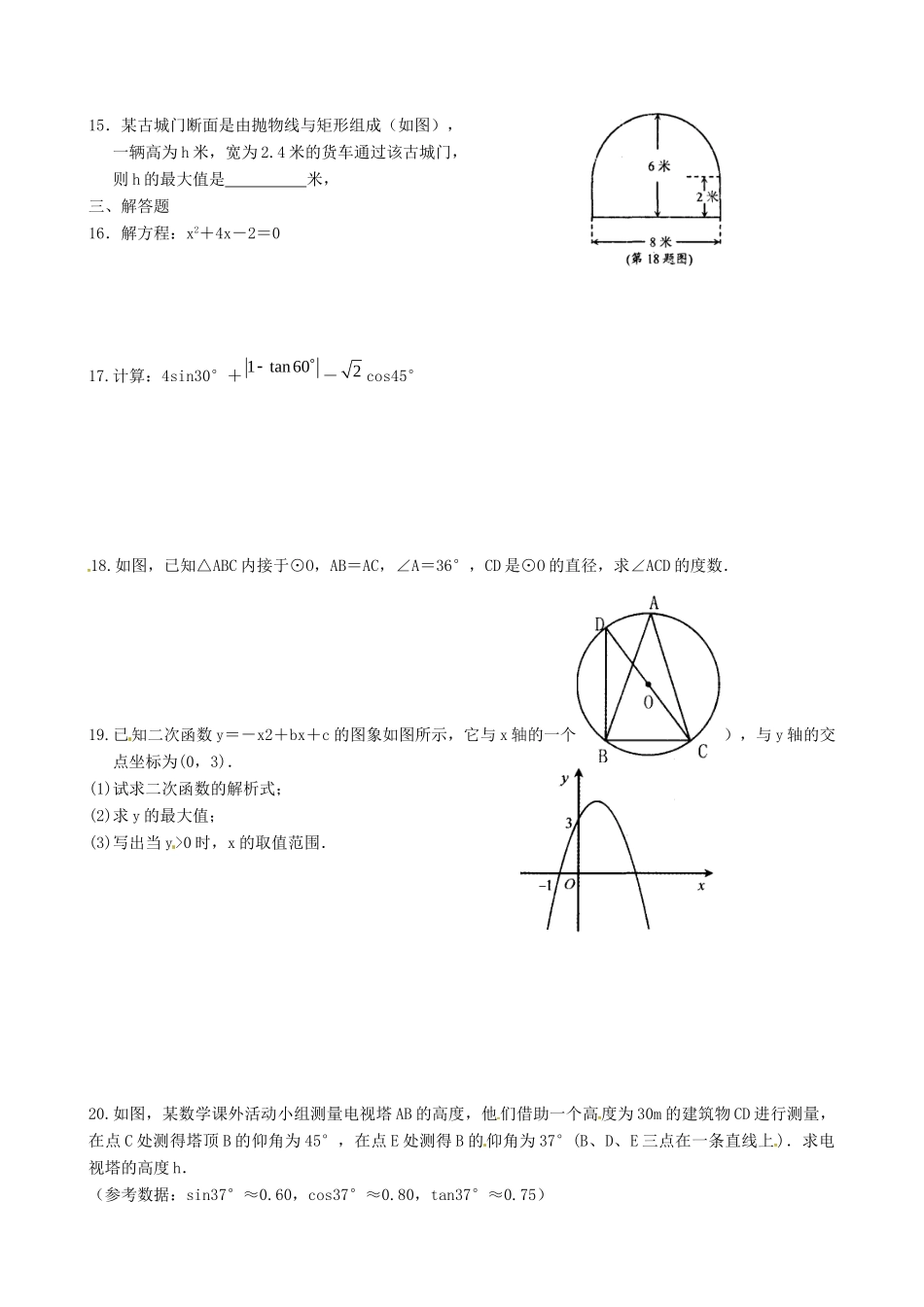
苏省灌南县实验中学2016届九年级数学上学期期末复习试题11班级姓名学号一.选择题:1.一元二次方程x(2x-1)=0的解是()A.x=0B.x=21C.x1=0,x2=21D.x1=0,x2=212.在Rt△ABC中,∠C=90°,若tanA=3,则∠A=()A.30°B.45°C.60°D.90°3.一元二次方程x2-23x+3=0的根的情况为()A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.没有实数根4.如图,⊙O的直径CD⊥弦AB,若∠A=40°,则∠CDB的度数为()A.25°B.30°C.40°D.50°5.二次函数221yxx与x轴的交点个数是()A.0B.1C.2D.36.两圆外切,圆心距为16cm,若两圆半径之比为5:3,则较小圆的半径是()A.3cmB.5cmC.6cmD.10cm7.已知二次函数y=ax2+bx+c的图象如图,则a、b、c满足()A.a<0,b<0,c>0;B.a<0,b<0,c<0;C.a<0,b>0,c>0;D.a>0,b<0,c>0.8.已知一个圆锥的侧面展开图是一个半径为4,圆心角为180°的扇形,则该圆锥的底面半径等于()A.1B.2C.3D.49.如图,在平面直角坐标系中,⊙P的圆心是(2,a)且(a>2)半径为2,函数y=x的图象被⊙P截得的弦AB的长为23,则a的值是()A.22B.2+2C.23D.2+3二、填空题10.抛物线y=-2(x-1)2+3有最_______值为_______.11.如图,CD是Rt△ABC斜边上的高,AC=8,BC=6.则cos∠BCD的值是_______.12.如图,是一水库大坝横断面的一部分,坝高h=5m,近水斜坡AB=10m,则这个斜坡的坡度i=________.13.如图,已知AB是⊙O的直径,MN是⊙O的切线,C是切点,连接AC,若∠CAB=50°,则∠ACN的度数为________.14.若二次函数y=ax2+3x+a2-1(a≠0的常数)的图象如图所示,则a的值为________.15.某古城门断面是由抛物线与矩形组成(如图),一辆高为h米,宽为2.4米的货车通过该古城门,则h的最大值是米,三、解答题16.解方程:x2+4x-2=017.计算:4sin30°+1tan60-2cos45°18.如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.19.已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).(1)试求二次函数的解析式;(2)求y的最大值;(3)写出当y>0时,x的取值范围.20.如图,某数学课外活动小组测量电视塔AB的高度,他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)21.在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC相切于一点E,连接DE并延长,与BC的延长线交于点F.(1)求证:BD=BF;(2)若DE=5,CF=1,试求⊙O的直径.22.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,此时拱桥的顶端点O距离水面4米.(1)建立如图所示的直角坐标系,利用待定系数法求出此抛物线的解析式;(2)当水位在正常水位时,有一只宽为8米的货船经过该桥,船上装有高出水面3.5米的长方体货物(货物与货船同宽).问:此船能否安全通过这座拱桥?