九年级数学上学期期中复习(6) 苏科版试卷VIP免费

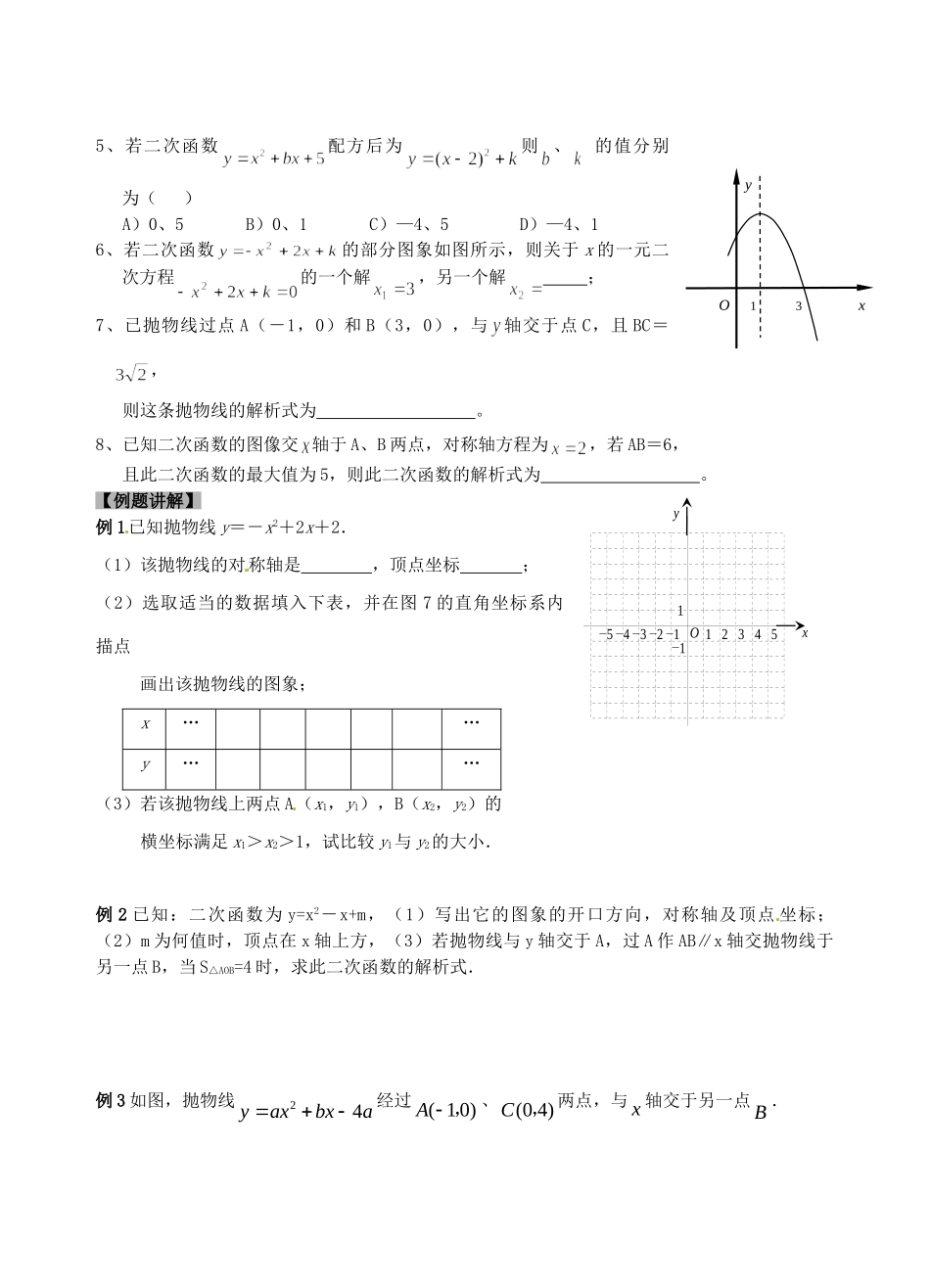
江苏省昆山市兵希中学九年级数学上学期期中复习（6）（无答案）苏科版【知识回顾】1．二次函数概念：如果：y＝ax2＋bx＋c(a≠0)，那么y叫做x的二次函数．2．二次函数2()yaxhk的图象和性质：a>0a<0开口方向顶点坐标、对称轴最值当x＝时，y有最值=当x＝时，y有最值=增减性在对称轴左侧y随x的增大而；y随x的增大而；在对称轴右侧y随x的增大而；y随x的增大而．3.二次函数2()yaxhk的图象的平移规律：4.二次函数cbxaxy2用配方法可化成khxay2的形式，其中h＝，k＝.5.二次函数cbxaxy2中cba,,与Δ的符号的确定：6．二次函数与一元二次方程的关系：7．待定系数法求二次函数的解析式：【基础训练】1、已知是二次函数，则m=．2、二次函数2(1)2yx的开口，顶点坐标，对称轴，当x=时y有最值=，当x时y随x的增大而增大，当x时y随x的增大而减小.3、把3)2(2xy向左平移3个单位，再向下平移3个单位可得抛物线．4、二次函数的图像如图所示，OA＝OC，则下列结论：①＜0；②；③；④；⑤；⑥。其中正确的有（）A、2个B、3个C、4个D、5个yx-21CBAO-5-4-3-2-1O12345xy-11yOx135、若二次函数配方后为则、的值分别为（）A）0、5B）0、1C）—4、5D）—4、16、若二次函数的部分图象如图所示，则关于x的一元二次方程的一个解，另一个解；7、已抛物线过点A（－1，0）和B（3，0），与轴交于点C，且BC＝，则这条抛物线的解析式为。8、已知二次函数的图像交轴于A、B两点，对称轴方程为，若AB＝6，且此二次函数的最大值为5，则此二次函数的解析式为。【例题讲解】例1已知抛物线y＝－x2＋2x＋2．（1）该抛物线的对称轴是，顶点坐标；（2）选取适当的数据填入下表，并在图7的直角坐标系内描点画出该抛物线的图象；x……y……（3）若该抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足x1＞x2＞1，试比较y1与y2的大小．例2已知：二次函数为y=x2－x+m，（1）写出它的图象的开口方向，对称轴及顶点坐标；（2）m为何值时，顶点在x轴上方，（3）若抛物线与y轴交于A，过A作AB∥x轴交抛物线于另一点B，当S△AOB=4时，求此二次函数的解析式．例3如图，抛物线24yaxbxa经过(10)A，、(04)C，两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）已知点(1)Dmm，在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；（3）在（2）的条件下，连接BD，点P为抛物线上一点，且45DBP°，求点P的坐标．【练习巩固】把它配方成y＝a(x-h)2＋k形式.(1)写出它的开口方向、顶点M的坐标、对称轴方程和最值；(2)求出图象与y轴、x轴的交点坐标；(3)x取什么值时y＞0，y＜0；(4)设图象交x轴于A，B两点，求△AMB面积．【课外作业】一、选择题：1.抛物线22()yxmn（mn，是常数）的顶点坐标是（）A．()mn，B．()mn，C．()mn，D．()mn，2.根据下表中的二次函数cbxaxy2的自变量x与函数y的对应值，可判断二次函数的图像与x轴（）A．只有一个交点B．有两个交点，且它们分别在y轴两侧C．有两个交点，且它们均在y轴同侧D．无交点3.函数y=ax＋1与y=ax2＋bx＋1（a≠0）的图象可能是（）x…－1012…y…－147－247…A．B．C．D．1111xoyyoxyoxxoy4.二次函数cbxaxy2的图象如图所示，若点A（1，y1）、B（2，y2）是它图象上的两点，则y1与y2的大小关系是（）A．21yyB．21yyC．21yyD．不能确定5.将函数2yxx的图象向右平移a(0)a个单位，得到函数232yxx的图象，则a的值为（）A．1B．2C．3D．46.在平面直角坐标系中，先将抛物线22yxx关于x轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（）A．22yxxB．22yxxC.22yxxD．22yxx7.如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是.二、填空题：1、若把代数式223xx化为2xmk的形式，则mk=.2.已知二次函数的图象经过原点及点（12，14），且图象与x轴的另一交点yxO3x=1到原点的距离为1，则该二次函数的解析式为3.抛物...