高考数学总复习 高考达标检测（十）函数零点的命题3角度-求个数、定区间、求参数 理-人教版高三全册数学试题VIP免费

高考达标检测（十）函数零点的命题3角度——求个数、定区间、求参数一、选择题1．(2017·烟台模拟)函数f(x)＝ln(x＋1)－的一个零点所在的区间是()A．(0,1)B．(1,2)C．(2,3)D．(3,4)解析：选B f(x)在(0，＋∞)上为增函数，且f(1)＝ln2－1<0，f(2)＝ln3－>0，∴f(x)的零点所在区间为(1,2)，故选B.2．(2017·吉林白山模拟)已知函数f(x)＝则函数g(x)＝f(x)－x的零点为()A．0B．－1，－2C．－1,0D．－2，－1,0解析：选B当x>1时，g(x)＝f(x)－x＝0，则2x－x＝0. 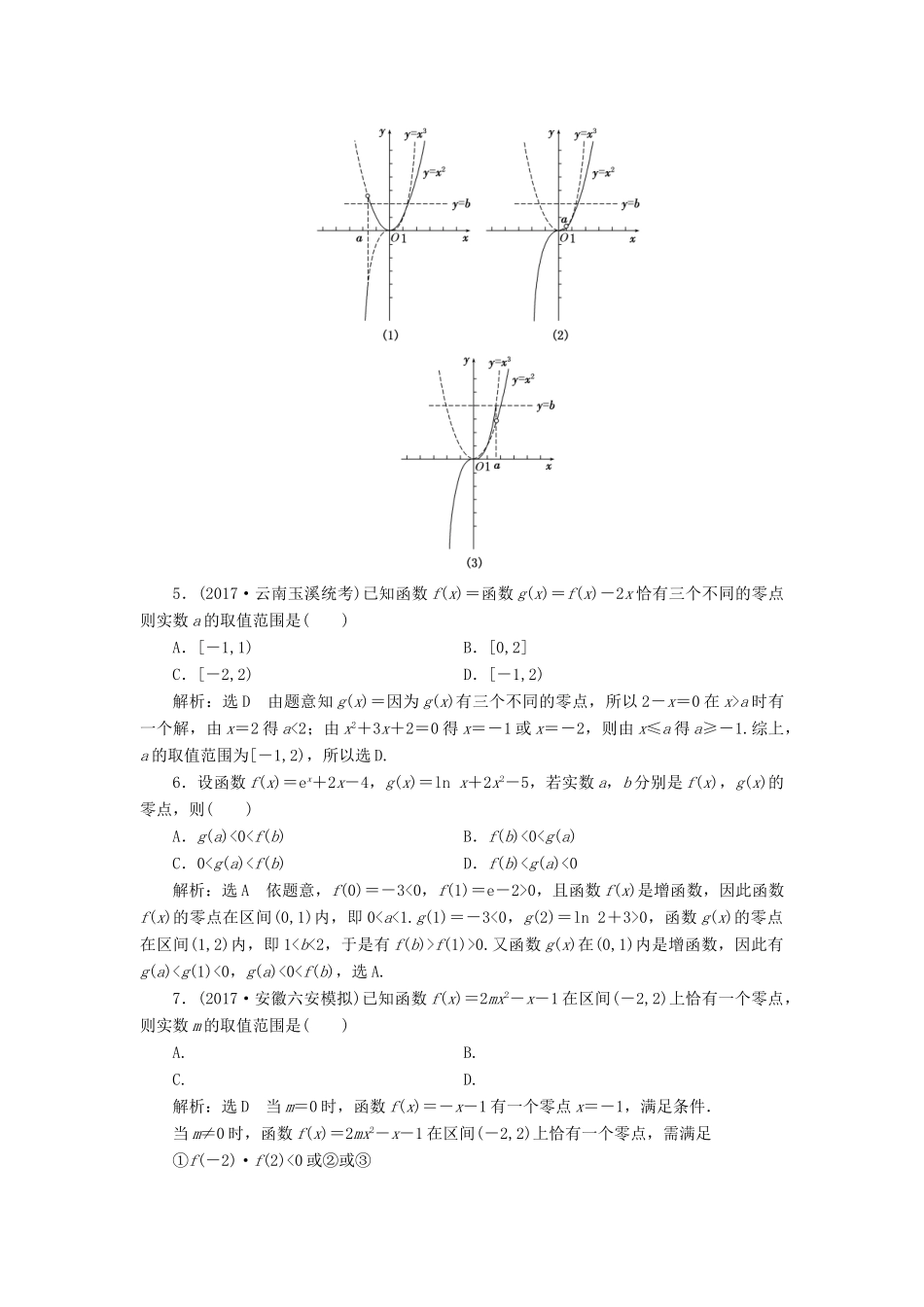x>1，∴此时方程无解；当x≤1时，g(x)＝f(x)－x＝x2＋3x＋2＝0，则x1＝－1或x2＝－2.综上，函数g(x)的零点为－1，－2.3．(2016·河南周口二模)已知函数f(x)＝x－log3x，若x0是函数y＝f(x)的零点，且0f(x0)．又x0是函数f(x)的零点，因此f(x0)＝0，所以f(x1)>0，即此时f(x1)的值恒为正值，选A.4．(2015·湖南高考)已知函数f(x)＝若存在实数b，使函数g(x)＝f(x)－b有两个零点，则a的取值范围是()A．[0,1]B．(－∞，0)C．(1，＋∞)D．(－∞，0)∪(1，＋∞)解析：选D函数g(x)有两个零点，即方程f(x)－b＝0有两个不等实根，则函数y＝f(x)和y＝b的图象有两个公共点．①若a<0，则当x≤a时，f(x)＝x3，函数单调递增；当x>a时，f(x)＝x2，函数先单调递减后单调递增，f(x)的图象如图(1)实线部分所示，其与直线y＝b可能有两个公共点．②若0≤a≤1，则a3≤a2，函数f(x)在R上单调递增，f(x)的图象如图(2)实线部分所示，其与直线y＝b至多有一个公共点．③若a>1，则a3>a2，函数f(x)在R上不单调，f(x)的图象如图(3)实线部分所示，其与直线y＝b可能有两个公共点．综上，a<0或a>1.5．(2017·云南玉溪统考)已知函数f(x)＝函数g(x)＝f(x)－2x恰有三个不同的零点则实数a的取值范围是()A．[－1,1)B．[0,2]C．[－2,2)D．[－1,2)解析：选D由题意知g(x)＝因为g(x)有三个不同的零点，所以2－x＝0在x>a时有一个解，由x＝2得a<2；由x2＋3x＋2＝0得x＝－1或x＝－2，则由x≤a得a≥－1.综上，a的取值范围为[－1,2)，所以选D.6．设函数f(x)＝ex＋2x－4，g(x)＝lnx＋2x2－5，若实数a，b分别是f(x)，g(x)的零点，则()A．g(a)<00，且函数f(x)是增函数，因此函数f(x)的零点在区间(0,1)内，即00，函数g(x)的零点在区间(1,2)内，即1f(1)>0.又函数g(x)在(0,1)内是增函数，因此有g(a)