高二数学上学期期未模拟试卷苏教版必修3VIP免费

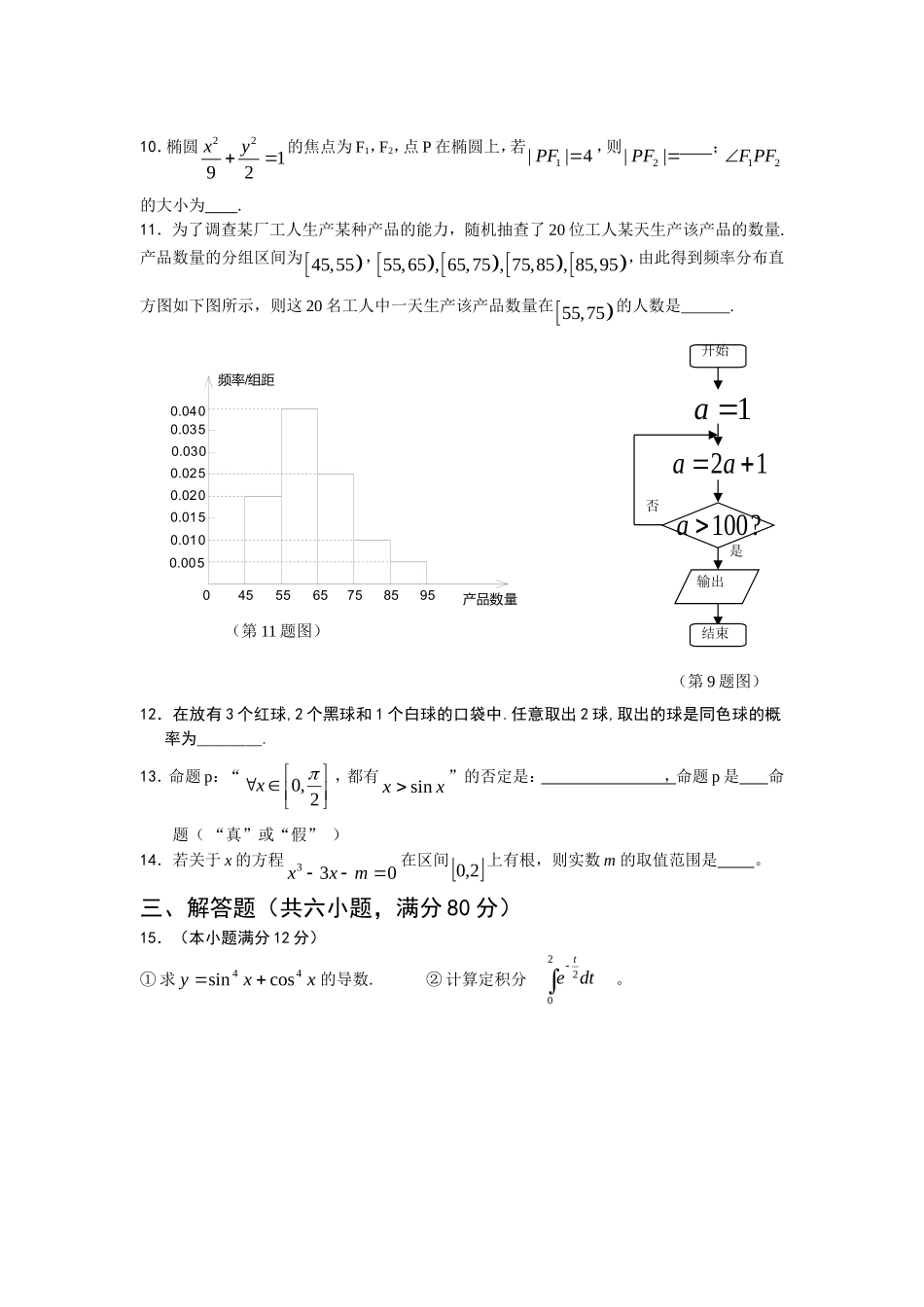
高二（理科）期未模拟试卷姓名学号班级一选择题（每小题5分，共8小题，满分40分）1．已知条件p：1x<2，条件q：2x－5x－6<0，则p是q的【】A充分必要条件B充分不必要条件C必要不充分条件D既不充分又不必要条件2．抛物线xy82的焦点坐标是【】A（-2,0）B（0,-2）C（-4,0）D（0,-4）3．已知函数xkxfcos)(的图象经过点P（3，1），则函数图象上过点P点的切线斜率等于【】A1B3C3D-14．在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若11ABa�,bDA11，cAA1，则下列向量中与MB1相等的向量是【】Acba2121Bcba2121Ccba2121Dcba21215．若双曲线222213xyaoa的离心率为2，则a等于【】A2B3C32D16．从数字1,2,3,4,5中任取两个不同的数字,构成一个两位数,则这个数大于40的概率是【】A25B45C15D357．设0,，则方程22sincos1xy不能表示的曲线为【】A椭圆B双曲线C抛物线D圆8．函数xexxf)3()(的单调递增区间是【】A)2,(B(0,3)C(1,4)D),2(w.w.w.k.s.5.u.c.o.m二、填空题（每小题5分，共6小题，满分30分）9．运行如图（右下）流程图，其输出结果是10．椭圆22192xy的焦点为F1，F2，点P在椭圆上，若1||4PF，则2||PF；12FPF的大小为.11．为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为45,55，55,65,65,75,75,85,85,95，由此得到频率分布直方图如下图所示，则这20名工人中一天生产该产品数量在55,75的人数是.产品数量频率/组距95857565554500.0400.0350.0300.0250.0200.0150.0100.00512．在放有3个红球,2个黑球和1个白球的口袋中.任意取出2球,取出的球是同色球的概率为________.13．命题p：“2,0x，都有xxsin”的否定是：，命题p是命题（“真”或“假”）14．若关于x的方程033mxx在区间2,0上有根，则实数m的取值范围是。三、解答题（共六小题，满分80分）15．（本小题满分12分）①求xxy44cossin的导数.②计算定积分dtet202。开始1a21aa100?a输出结束是否（第9题图）（第11题图）16.（本小题满分13分）为了测试某批灯光的使用寿命,从中抽取了20个灯泡进行试验,记录如下：(以小时为单位)171、159、168、166、170、158、169、166、165、162168、163、172、161、162、167、164、165、164、167⑴列出样本频率分布表；⑵画出频率分布直方图；⑶从频率分布的直方图中,估计这些灯泡的使用寿命。17．（本小题满分12分）在抛物线y=x2上求一点P,使得点P到直线x-y-3=0的距离最短，并求出最短距离。18．（本小题满分14分）口袋中有质地、大小完全相同的3个球，编号分别为1，2，3，甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢．（1）求甲赢且编号的和为4的事件发生的概率；（2）这种游戏规则公平吗？试说明理由．19（本小题满分14分）如图，直三棱柱ABC-A1B1C1底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2,M，N分别是A1B1，A1A的中点。（1）求BN的长度；（2）求cos（1BA，1CB）的值；（3）求证：A1B⊥C1M。20.（本小题满分15分）设函数baxxxf3)(3，若曲线()yfx在点(2,())fx处与直线8y相切（Ⅰ）求a，b的值；（Ⅱ）求函数()fx的单调区间与极值点；（Ⅲ）求函数f(x)在区间3,0上的最值。