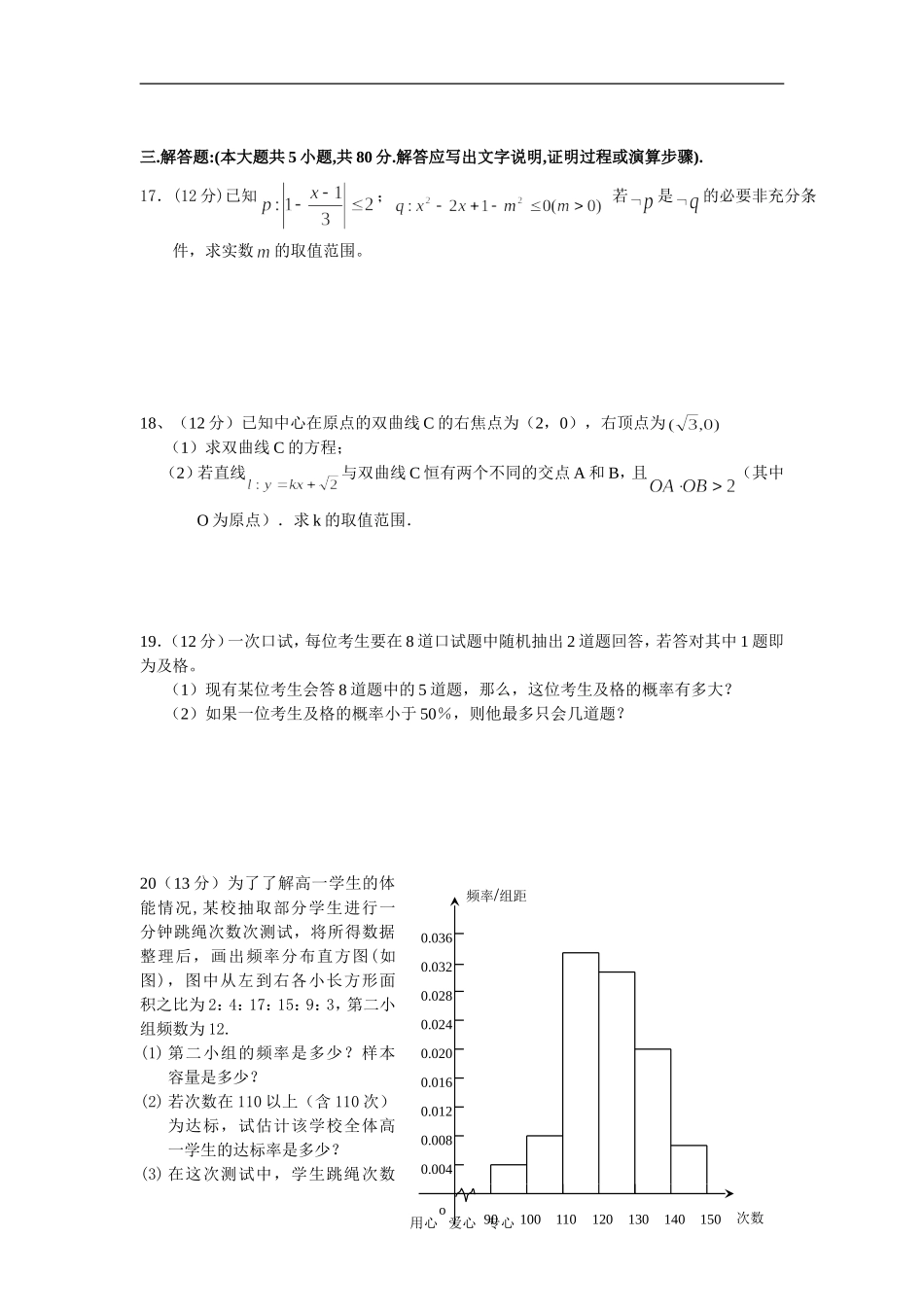
2007—2008学年度第一学期南通市五校联考高二年级(文科)数学学科期中试题时间:120分钟分值:160分命题人:薛窑中学陆建兵第Ⅰ卷选择题(共50分)一.选择题:(本大题共10小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的).1.从一批产品中取出三件,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论正确的是()A.A与C互斥B.B与C互斥C.任两个均互斥D.任两个均不互斥2下面伪代码的输出结果为()S←1ForIfrom1to9step2S←S+IEndforPrintSA.45B.23C.25D.263.在抽查某产品尺寸过程中,将其尺寸分成若干组,[a,b]是其中的一组,已知该组的频率为m,该组上的直方图的高为h,则等于()A.mhB.C.D.m+h4.有以下四个命题,其中真命题的是()①“若,则互为倒数”的逆命题;②“相似三角形的周长相等”的否命题;③“若,则方程有实根”的逆否命题;④“若,则”的逆否命题.A.①②B.②③C.①③D.③④5、A是圆上固定的一点,在圆周上等可能地任取一点与A连结,弦长超过半径的概率为()A.B.C.D.6、已知,点P在A、B所在的平面内运动且保持,则的最大值和最小值分别是()A.、3B.10、2C.5、1D.6、47.已知为抛物线上一动点,为抛物线的焦点,定点,则的最小值为()A.3B.4C.5D.6用心爱心专心8.若,则“”是“”成立的()A.充分条件B.必要条件C.充要条件D.既非充分也非必要条件9.已知双曲线的实轴长、虚轴长、焦距长成等差数列,则双曲线的离心率e为()A.2B.3C.D.10、若双曲线与的离心率分别为,则当变化时,的最小值是()A.B.C.D.第Ⅱ卷非选择题部分(共110分)二.填空题:(本大题共6小题;每小题5分,共30分.把答案填在题中横线上)11.1.已知关于某设备的使用年限与所支出的维修费用(万元),有如下统计资料:使用年限23456维修费用2.23.85.56.57.0若对呈线性相关关系,则线性回归方程表示的直线一定过定点__________.12.用辗转相除法求两个数102、238的最大公约数是__________.13.若“或”是假命题,则的范围是___________。14.箱子中装有红、白、黑色球各1个,现每次任取1个,有放回地抽取3次,则三种颜色都被取过一次的概率为..15.,底面直径为的圆柱被与底面成30°的平面所截,其截口是一个椭圆,则这个椭圆的离心率为.16.若方程所表示的曲线为C,给出下列四个命题:①若C为椭圆,则14或t<1;③曲线C不可能是圆;④若C表示椭圆,且长轴在x轴上,则.其中真命题的序号为(把所有正确命题的序号都填在横线上)用心爱心专心三.解答题:(本大题共5小题,共80分.解答应写出文字说明,证明过程或演算步骤).17.(12分)已知;若是的必要非充分条件,求实数的取值范围。18、(12分)已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(1)求双曲线C的方程;(2)若直线与双曲线C恒有两个不同的交点A和B,且(其中O为原点).求k的取值范围.19.(12分)一次口试,每位考生要在8道口试题中随机抽出2道题回答,若答对其中1题即为及格。(1)现有某位考生会答8道题中的5道题,那么,这位考生及格的概率有多大?(2)如果一位考生及格的概率小于50%,则他最多只会几道题?20(13分)为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(3)在这次测试中,学生跳绳次数用心爱心专心90100110120130140150次数o0.0040.0080.0120.0160.0200.0240.028频率/组距0.0320.036的中位数落在哪个小组内?请说明理由。21.(15分)下面是关于某一算式的三个流程图:(1)(2)(3)(I)请根据流程图(1)指出其算法功能(用算式表示),并分别指出流程图(2)、(3)判断框中的条件;(II)若分别交换三个流程图中S←S+I与I←I+2的位置,应如何调整各框中的条件,使其完成(I)中的算法功能?(不要重画流...