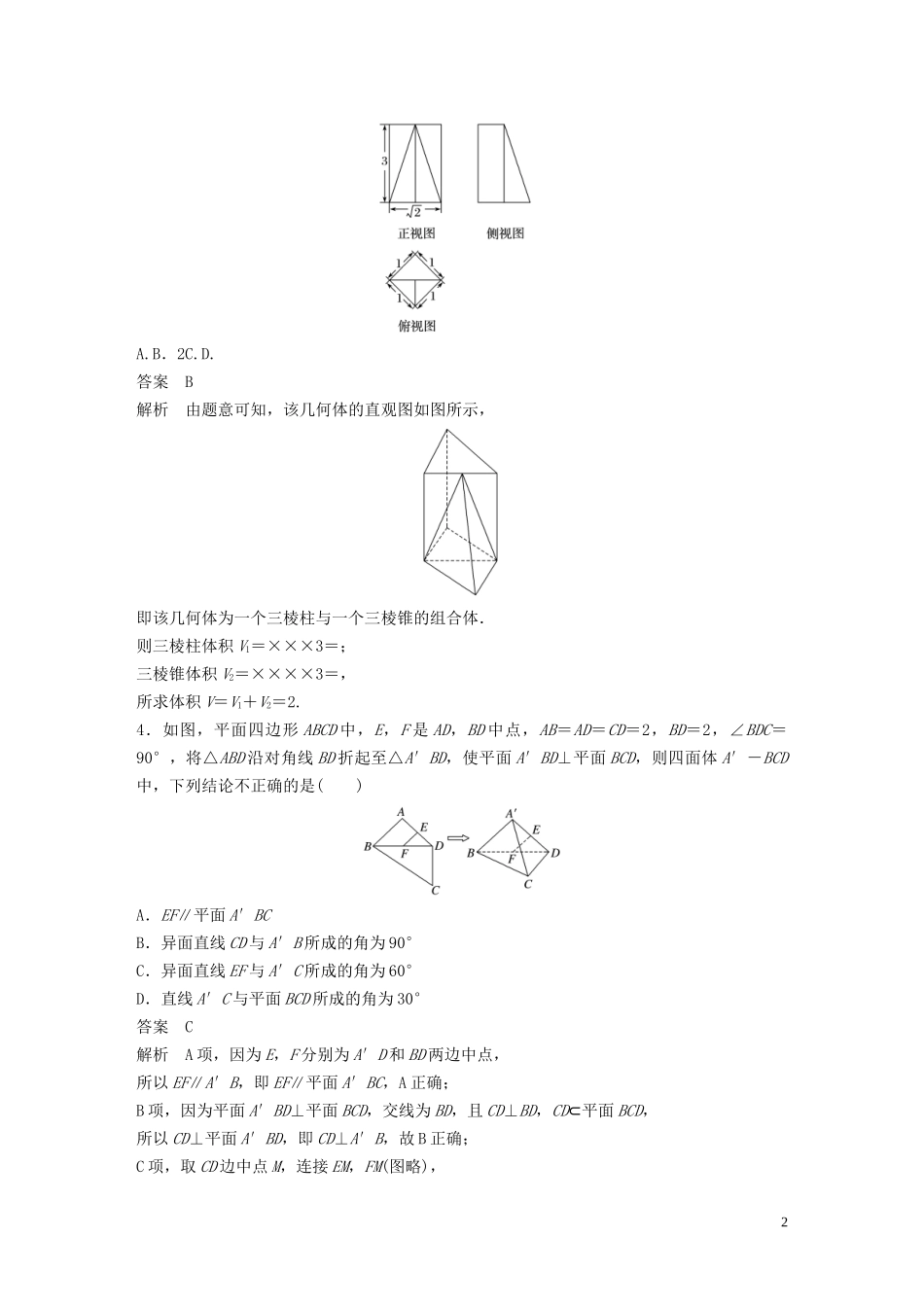
(三)立体几何1.(2019·浙江省三校联考)已知平面α,β,直线m,n,若α⊥β,α∩β=l,m⊂α,n⊂β,则“m⊥n”是“m,n中至少有一条与l垂直”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案C解析先判断充分性,当m⊥n时,假设m,n都不与l垂直.在平面α内作l的垂线m′,由α⊥β可得m′⊥β,则m′⊥n.由m′⊥l,m不垂直于l可得m′与m相交.由m′⊥n,m⊥n可得n⊥α.所以n⊥l,矛盾.所以当m⊥n时,可以推出m,n中至少有一条与l垂直,即充分性成立.再判断必要性,当m,n中至少有一条与l垂直时,不妨设m⊥l,由α⊥β可得m⊥β,所以m⊥n,即必要性成立.综上所述,“m⊥n”是“m,n中至少有一条与l垂直”的充要条件.故选C.2.某几何体的三视图如图所示,其中俯视图右侧曲线为半圆弧,则该几何体的表面积为()A.3π+4-2B.3π+2-2C.+2-2D.+2+2答案A解析由三视图还原出原几何体是一个半圆柱挖去一个三棱柱,尺寸见三视图,S=π×1×2+2×+2××2=3π-2+4,故选A.3.已知某几何体是由一个三棱柱和一个三棱锥组合而成的,其三视图如图所示,则该几何体的体积为()1A.B.2C.D.答案B解析由题意可知,该几何体的直观图如图所示,即该几何体为一个三棱柱与一个三棱锥的组合体.则三棱柱体积V1=×××3=;三棱锥体积V2=××××3=,所求体积V=V1+V2=2.4.如图,平面四边形ABCD中,E,F是AD,BD中点,AB=AD=CD=2,BD=2,∠BDC=90°,将△ABD沿对角线BD折起至△A′BD,使平面A′BD⊥平面BCD,则四面体A′-BCD中,下列结论不正确的是()A.EF∥平面A′BCB.异面直线CD与A′B所成的角为90°C.异面直线EF与A′C所成的角为60°D.直线A′C与平面BCD所成的角为30°答案C解析A项,因为E,F分别为A′D和BD两边中点,所以EF∥A′B,即EF∥平面A′BC,A正确;B项,因为平面A′BD⊥平面BCD,交线为BD,且CD⊥BD,CD⊂平面BCD,所以CD⊥平面A′BD,即CD⊥A′B,故B正确;C项,取CD边中点M,连接EM,FM(图略),2则EM∥A′C,所以∠FEM为直线A′C与异面直线EF所成角,又EF=1,EM=,FM=,即∠FEM=90°,故C错误,D项,因为平面A′BD⊥平面BCD,连接A′F,则A′F⊥BD,所以A′F⊥平面CBD,连接FC,所以∠A′CF为直线A′C与平面BCD所成角,又CD⊥A′D,所以A′C=2,又A′F==,sin∠A′CF===,所以∠A′CF=30°,D正确.5.如图,长方体ABCD-A1B1C1D1,以A为球心,AA1,AB,AD,AC1为半径作四个同心球,其体积依次为V1,V2,V3,V4,表面积依次为S1,S2,S3,S4,则有()A.V1+V2+V3=V4且S1+S2+S3=S4B.V1+V2+V3>V4且S1+S2+S3≠S4C.V1+V2+V3