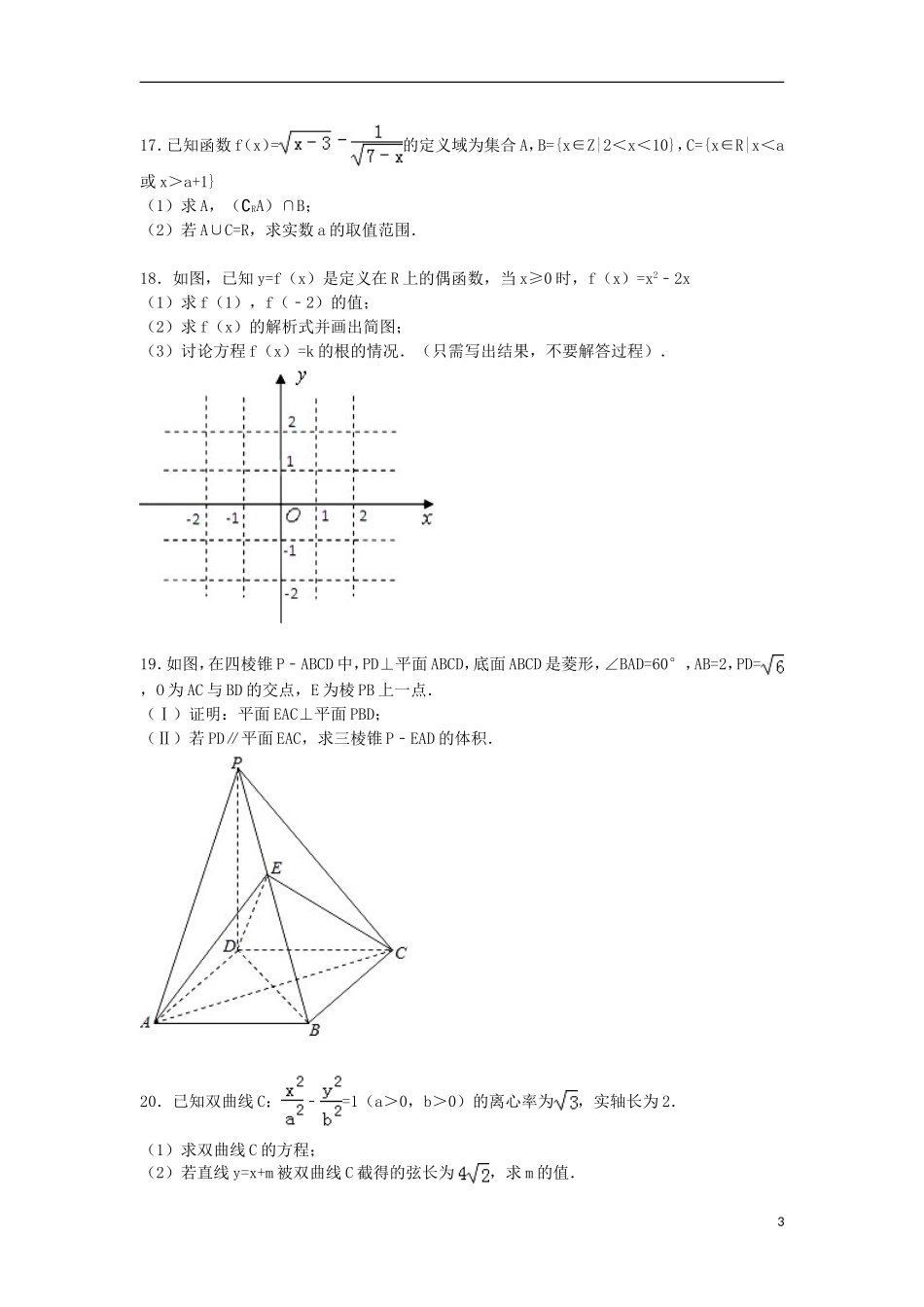
2015-2016学年湖南省株洲十八中高二(上)期末数学试卷(理科)(B卷)一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.命题“∃x∈R,使x>1”的否定是()A.∀x∈R,都有x>1B.∃x∈R,使x<1C.∀x∈R,都有x≤1D.∃x∈R,使x≤12.“x=1”是“x2﹣3x+2=0”成立的()A.充分而不必要条件B.必要而不充分条件C.充分且必要条件D.既不充分也不必要条件3.已知函数f(x)=,则f(f(5))的值为()A.1B.2C.3D.44.已知椭圆的两个焦点为F1,F2,弦AB过点F1,则△ABF2的周长为()A.10B.16C.20D.365.下列函数是偶函数的是()A.y=xB.y=2x2﹣3C.D.y=x2,x∈[0,1]6.已知向量=(1,1,0),=(﹣1,0,2),且与互相垂直,则k的值是()A.1B.C.D.7.如图:在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若,,,则下列向量中与相等的向量是()A.B.C.D.18.已知函数f(x)是定义在区间[0,+∞)上的增函数,则满足f(2x﹣1)<f()的x的取值范围是()A.(,)B.[,)C.(,)D.[,)9.曲线=1与曲线=1(k<9)的()A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等10.由直线x=,x=2,曲线y=﹣及x轴所围图形的面积为()A.﹣2ln2B.2ln2C.D.11.如果函数f(x)对任意a,b满足f(a+b)=f(a)•f(b),且f(1)=2,则=()A.1006B.2010C.2016D.403212.已知函数f(x)=﹣x3+ax2﹣x﹣1在(﹣∞,+∞)上是单调函数,则实数a的取值范围是()A.B.C.D.二、填空题:(本大题共4小题,每小题5分.共20分)13.已知向量,若,则x=;若则x=.14.曲线f(x)=x3+x﹣2在点P0处的切线平行于直线y=4x﹣1,则P0点坐标为.15.已知函数=.16.已知点M是y=上一点,F为抛物线的焦点,A在C:(x﹣1)2+(y﹣4)2=1上,则|MA|+|MF|的最小值为.三.解答题:(六个大题,共70分,解答应写出文字说明,证明过程或演算步骤.)217.已知函数f(x)=的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}(1)求A,(∁RA)∩B;(2)若A∪C=R,求实数a的取值范围.18.如图,已知y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x(1)求f(1),f(﹣2)的值;(2)求f(x)的解析式并画出简图;(3)讨论方程f(x)=k的根的情况.(只需写出结果,不要解答过程).19.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=,O为AC与BD的交点,E为棱PB上一点.(Ⅰ)证明:平面EAC⊥平面PBD;(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.20.已知双曲线C:﹣=1(a>0,b>0)的离心率为,实轴长为2.(1)求双曲线C的方程;(2)若直线y=x+m被双曲线C截得的弦长为,求m的值.321.已知函数f(x)=lnx,g(x)=ax2﹣bx(a、b为常数).(1)求函数f(x)在点(1,f(1))处的切线方程;(2)当函数g(x)在x=2处取得极值﹣2.求函数g(x)的解析式;(3)当时,设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围.22.设a∈R,已知函数f(x)=ax3﹣3x2.(Ⅰ)当a=1时,求函数f(x)的单调区间;(Ⅱ)若对任意的x∈[1,3],有f(x)+f′(x)≤0恒成立,求实数a的取值范围.42015-2016学年湖南省株洲十八中高二(上)期末数学试卷(理科)(B卷)参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.命题“∃x∈R,使x>1”的否定是()A.∀x∈R,都有x>1B.∃x∈R,使x<1C.∀x∈R,都有x≤1D.∃x∈R,使x≤1【考点】特称命题;命题的否定.【专题】计算题.【分析】根据命题“∃x∈R,使得x>1”是特称命题,其否定为全称命题,即∀x∈R,使得x≤1,从而得到答案.【解答】解: 命题“∃x∈R,使得x>1”是特称命题∴否定命题为:∀x∈R,使得x≤1故选C.【点评】这类问题的常见错误是没有把全称量词改为存在量词,或者对于“>”的否定用“<”了.这里就有注意量词的否定形式.如“都是”的否定是“不都是”,而不是“都不...