九年级数学上册 二次函数每日一练(四)、(五)(新版)新人教版试卷VIP免费

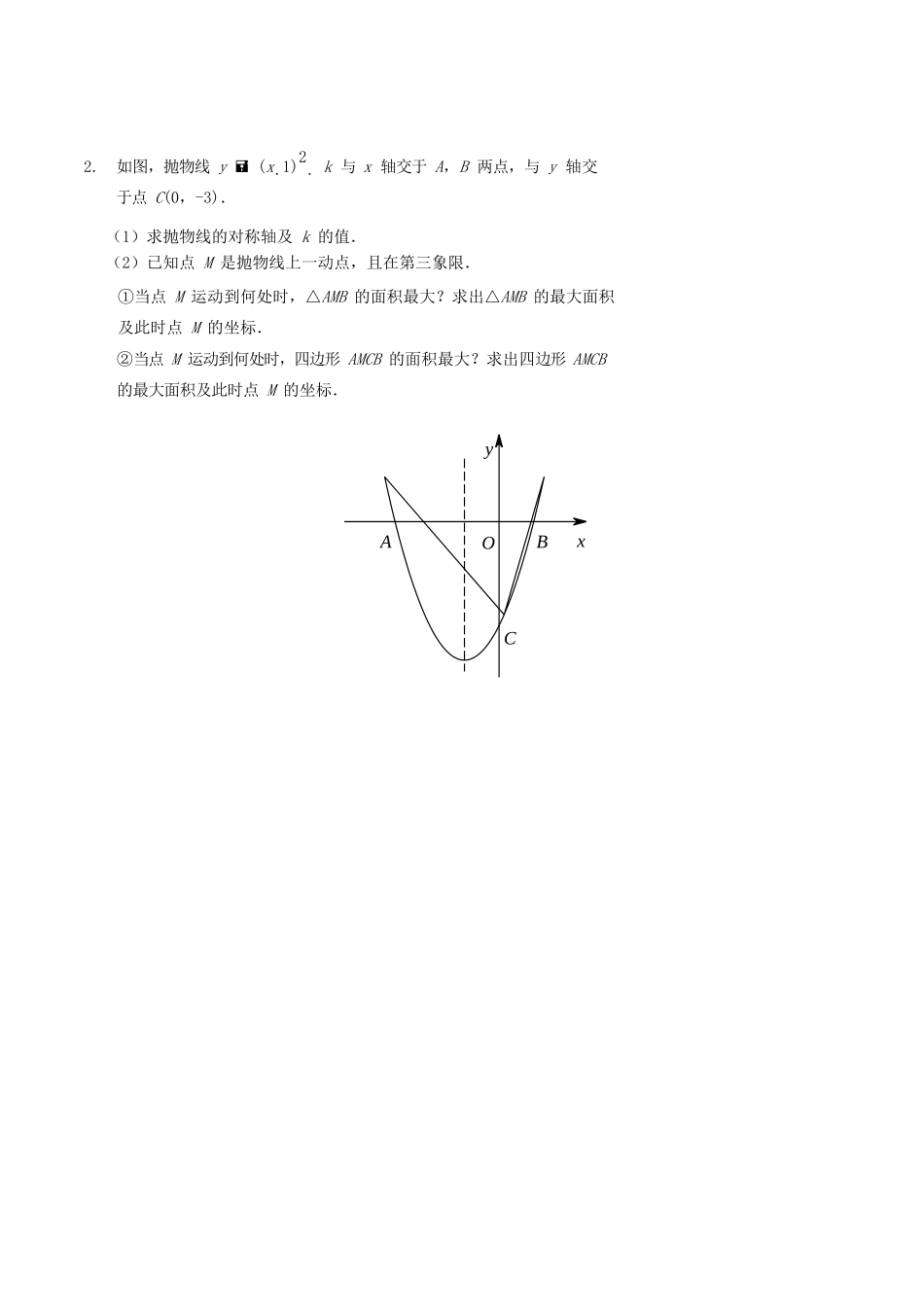
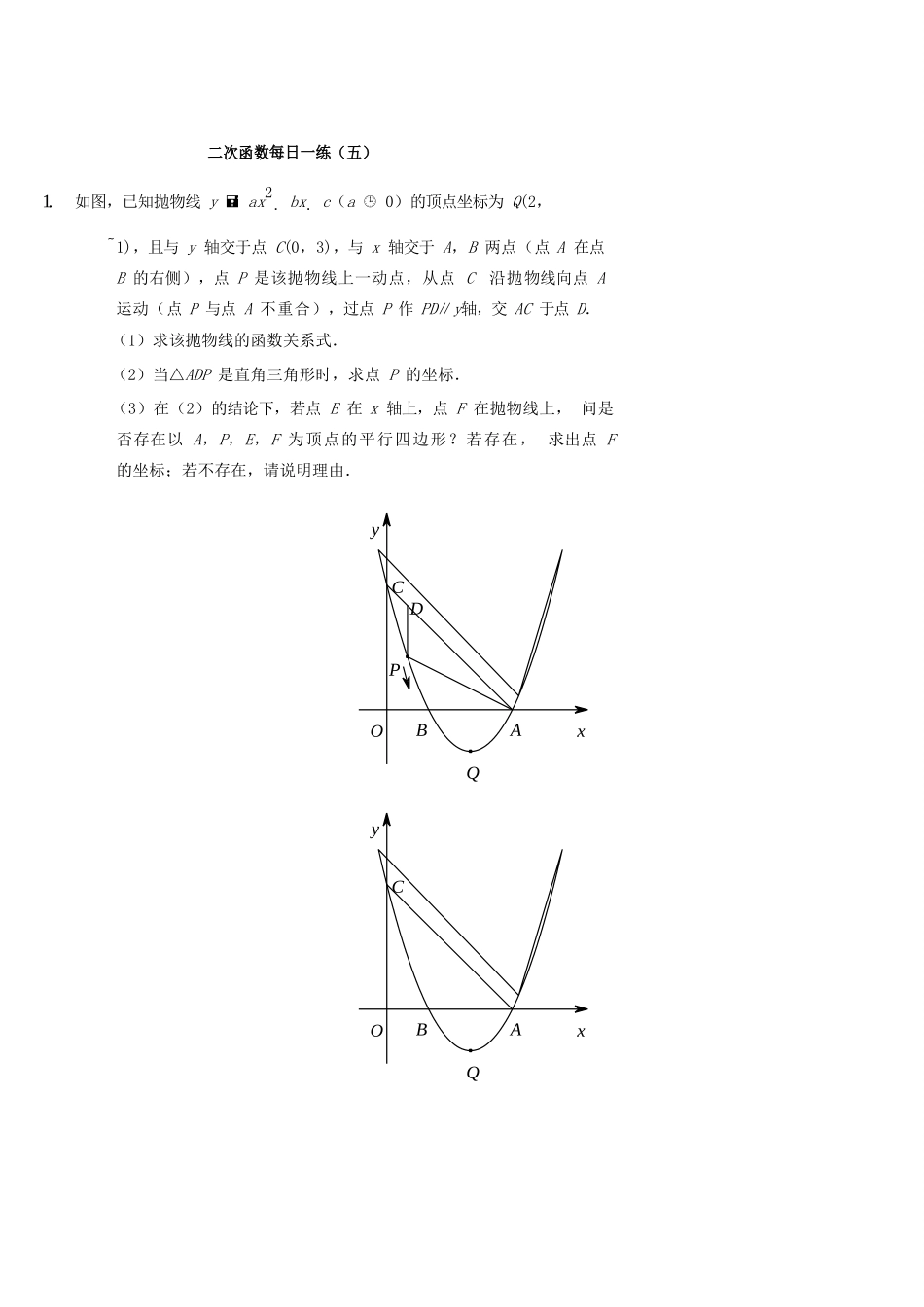
二次函数每日一练（四）1.如图，已知抛物线经过A(-1，0)，B(3，0)，C(0，3)三点．（1）求抛物线的解析式．（2）M是线段BC上一点（不与点B，C重合），过点M作MN∥y轴，交抛物线于点N，若点M的横坐标为m，请用含m的代数式表示线段MN的长．（3）在（2）的条件下，连接NB，NC，是否存在点M，使△BNC的面积最大？若存在，求出m的值；若不存在，请说明理由．yNCMAOBx2.如图，抛物线y(x1)2k与x轴交于A，B两点，与y轴交于点C(0，-3)．（1）求抛物线的对称轴及k的值．（2）已知点M是抛物线上一动点，且在第三象限．①当点M运动到何处时，△AMB的面积最大？求出△AMB的最大面积及此时点M的坐标．②当点M运动到何处时，四边形AMCB的面积最大？求出四边形AMCB的最大面积及此时点M的坐标．yAOBxC二次函数每日一练（五）1.如图，已知抛物线yax2bxc（a0）的顶点坐标为Q(2，1)，且与y轴交于点C(0，3)，与x轴交于A，B两点（点A在点B的右侧），点P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与点A不重合），过点P作PD∥y轴，交AC于点D．（1）求该抛物线的函数关系式．（2）当△ADP是直角三角形时，求点P的坐标．（3）在（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A，P，E，F为顶点的平行四边形？若存在，求出点F的坐标；若不存在，请说明理由．yCDPOBAxQyCOBAxQ2.在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，-4)，C(2，0)三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值；（3）若点P是抛物线上的动点，点Q是直线yx上的动点，判断有几个位置能够使得点P，Q，B，O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．yAOCxMByAOCxB12【参考答案】二次函数每日一练（四）1.（1）yx22x3；（2）MN=m23m（3）存在，m3，理由略22.（1）对称轴为直线x=-1，k4（2）①M(1，4)，S△AMB8②S75，M(3，15)四边形AMCB824二次函数每日一练（五）1.（1）y(x2)21（2）P(1，0)，P(2，1)（3）存在，F1(22.（1）y1x2x422，1)，F2(22，1)（2）Sm24m（m），最大值为（3）Q1(225，225)，Q2(4，4)Q3(225，225)，Q4(4，4)