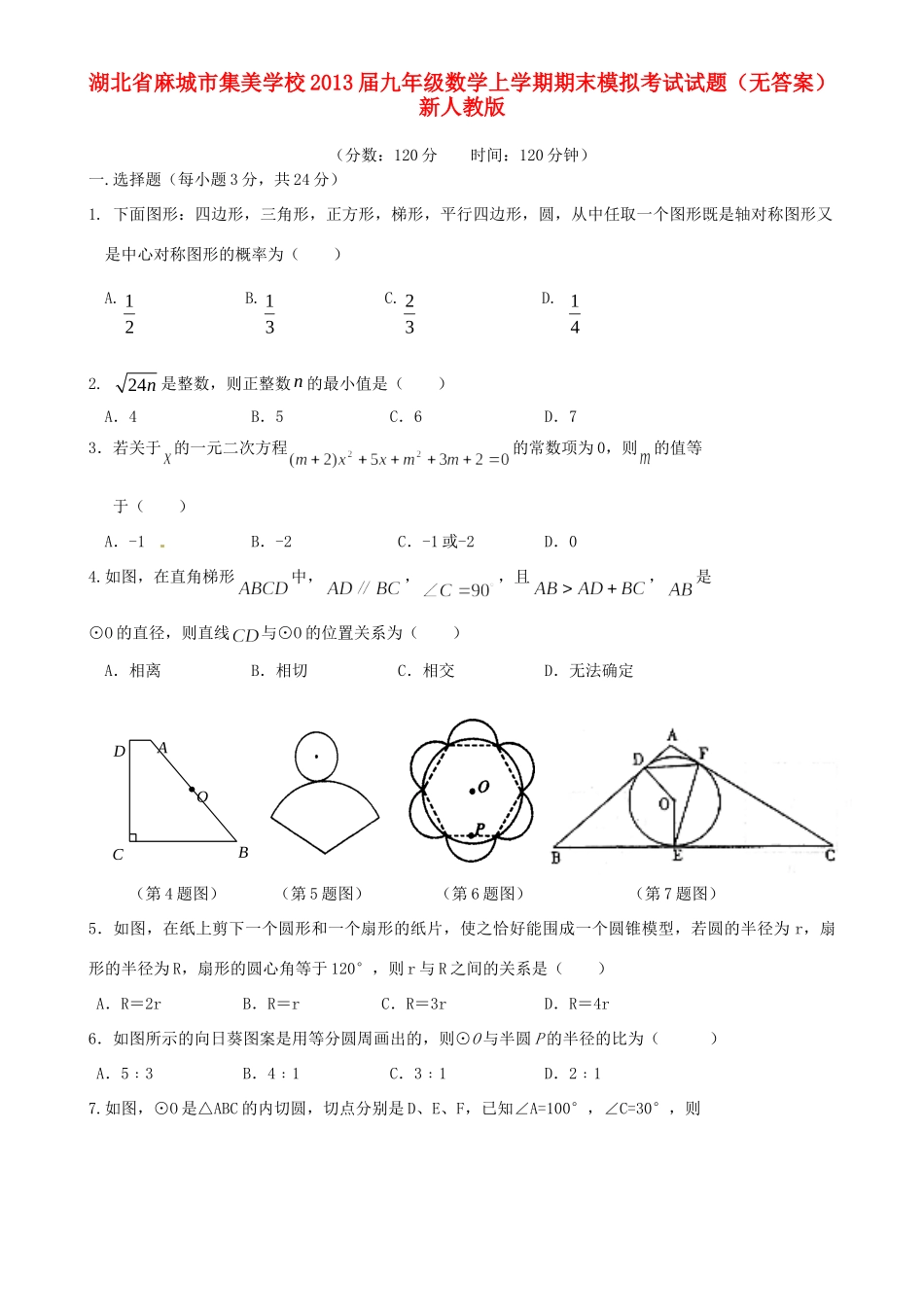
湖北省麻城市集美学校2013届九年级数学上学期期末模拟考试试题(无答案)新人教版(分数:120分时间:120分钟)一.选择题(每小题3分,共24分)1.下面图形:四边形,三角形,正方形,梯形,平行四边形,圆,从中任取一个图形既是轴对称图形又是中心对称图形的概率为()A.21B.31C.32D.412.24n是整数,则正整数n的最小值是()A.4B.5C.6D.73.若关于的一元二次方程的常数项为0,则的值等于()A.-1B.-2C.-1或-2D.04.如图,在直角梯形中,,,且,是⊙O的直径,则直线与⊙O的位置关系为()A.相离B.相切C.相交D.无法确定(第4题图)(第5题图)(第6题图)(第7题图)5.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的半径为R,扇形的圆心角等于120°,则r与R之间的关系是()A.R=2rB.R=rC.R=3rD.R=4r6.如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为()A.5﹕3B.4﹕1C.3﹕1D.2﹕17.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则ADCBO∠DFE的度数是()A.55°B.60°C.65°D.70°8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③a-b+c<0;④a+c>0,其中正确结论的个数为().A.1个B.2个C.3个D.4个(第8题)(第16题)二.填空题(每小题3分,共24分)9.在平面直角坐标系中,点(a,5)关于原点对称的点的坐标是(1,b+1),则点(a,b)在第象限.10.若式子有意义,则x的取值范围是.11.若关于x的一元二次方程0)2(32mxx没有实数根,则m的取值范围是__________.12.若⊙O1和⊙O2相交于点A、B,且AB=24,⊙O1的半径为13,⊙O2的半径为15,则O1O2的长为_________.13.如图,这是中央电视台“曲苑杂坛”中的一副图案,它是一扇形图形,其中为,长为8cm,长为12cm,则阴影部分的面积为.14.在一所4000人的学校随机调查了100人,其中有24人上学之前没有吃过早餐,则在这所学校里随便问一个人,上学之前吃过早餐的概率是.15.一个直角三角形的两条边的长是方程x2-14x+48=0的两个根,则此直角三角形的周长为.16.如图,将一个含有45°角的三角尺绕顶点C顺时针旋转135°后,顶点A所经过的路线与顶点B所经过的路线长的比值为.三、解答题(共72分)17.(每小题4分,共8分)(1)、化简(2)、解方程:4x2-4x+1=x2+6x+9ACOB(第13题)18.(本题满分8分)如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).(1)请直接写出点A关于y轴对称的点的坐标;(2)将△ABC绕坐标原点O顺时针旋转90°;画出图形,直接写出点B的对应点的坐标;(3)请直接写出:以A,B,C为顶点的平行四边形ABCD的第四个顶点D的坐标.19.(本题满分8分)已知关于x的一元二次方程x2+2(k-1)x+k2-1=0有两个不相等的实数根x1,x2.(1)求实数k的取值范围;(2)若3(x1+x2)=x1x2,求k的值.20.(本题满分8分)如图,在⊙O中,AB为⊙O的直径,AC是弦,4OC,60OAC.(1)求∠AOC的度数;(4分)(2)如图,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长.(4分)21.(本题满分8分)将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上.⑴从中随机抽取两张卡片,求卡片正面上的数字之和大于4的概率;⑵若先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,求组成的两位数恰好是3的倍数的概率(请用树形图或列举法加以说明).ACOPB22.(本题满分8分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.⑴当每辆车的月租金定为3600元时,能租出多少辆车?⑵当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?23.(本题满分12分)如图,AB是圆o的直径,AD、BC都垂直于AB,AD=13cm,BC=16cm,DC=5cm,点P、Q是动点,点...