高中数学 第二章 数列 2.1.1 数列课后训练 新人教B版必修5-新人教B版高二必修5数学试题VIP免费

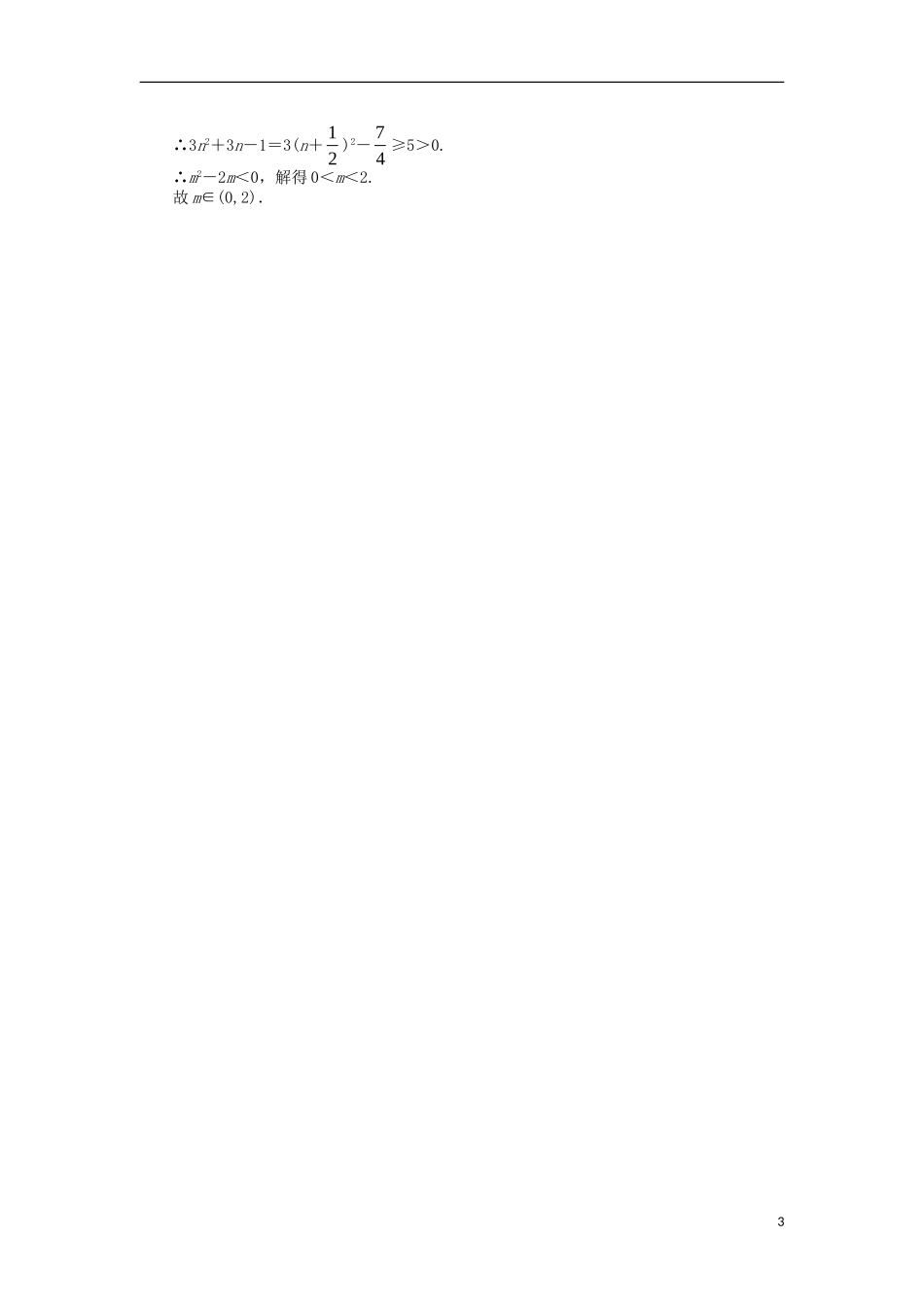
2.1.1数列课后训练1．数列0,1,0，－1,0,1,0，－1，…的一个通项公式为()．A．112nB．πcos2nC．1cosπ2nD．2cosπ2n2．已知数列2，5，22，11，…，则25是该数列的()．A．第6项B．第7项C．第10项D．第11项3．已知数列{an}的通项公式为an＝n2－8n＋15，则3()．A．不是数列{an}中的项B．只是数列{an}中的第2项C．只是数列{an}中的第6项D．是数列{an}中的第2项或第6项4．数列{an}的通项公式an＝log(n＋1)(n＋2)，则它的前30项之积是()．A．15B．5C．6D．231log3log3255．数列1，13，17，115，…的通项公式an是()．A．1(1)21nnB．1(1)21nnC．1121nnD．1121nn6．在某报《自测健康状况》的报道中，自测血压结果与相应年龄的统计数据如下表．观察表中数据的特点，用适当的数填入表中空白(______)内.年龄(岁)3035404550556065收缩压(水银柱/毫米)110115120125130135(____)145舒张压(水银柱/毫米)707375788083(____)887．数列123，145，187，1169，…的一个通项公式为________________．8．根据数列的前四项，写出数列的一个通项公式．(1)2,5,10,17，…；(2)112，123，134，145，….9．已知数列an＝(m2－2m)(n3－2n)是递减数列，求实数m的取值范围．1参考答案1.答案：D当n＝4时，4(1)1(1)11122n，π4πcoscos22n＝cos2π＝1≠－1，排除选项A，B；当n＝2时，(1)π3πcoscos0122n，排除选项C.故选D.2.答案：．B把22写成8，25写成20，由题意，可得31nan.令31253120nn3n－1＝20n＝7.3.答案：D令an＝3，即n2－8n＋15＝3，解得n＝2或n＝6.4.答案：Ba1a2…a30＝log23×log34×…×log3132＝lg3lg4lg32lg2lg3lg31＝log232＝log225＝5.5.答案：D(观察法)通项的符号为(－1)n－1，分子都是1，分母为1,3,7,15，…，其通项为2n－1.所以数列的通项公式为1(1)21nnna.(特值法)取n＝1代入选项A，B的通项公式，得项为－1，不合题意，可排除选项A，B.再取n＝3代入选项C的通项公式，得项为15，不合题意，可排除选项C.6.答案：140857.答案：an＝(－1)n－1(2n＋121n)各项的绝对值分别为11122233211211144255221，31118827723141111616299241，…，第n项的绝对值为1221nn；而奇数项为正，偶数项为负，故an＝(－1)n－1(2n＋121n)．8.答案：解：(1)如果数列的各项分别减去1，则变为1,4,9,16，…，所以通项公式为an＝n2＋1；(2)数列的前四项的分子都是1，分母是两个连续正整数的积，且奇数项为负，偶数项为正，所以通项公式为(1)(1)nnann.9.答案：解：∵数列{an}为递减数列，∴an＋1＜an.∴an＋1－an＝(m2－2m)[(n＋1)3－2(n＋1)－n3＋2n]＝(m2－2m)(3n2＋3n－1)＜0.∵n∈N＋，2∴3n2＋3n－1＝3(n＋12)2－74≥5＞0.∴m2－2m＜0，解得0＜m＜2.故m∈(0,2)．3