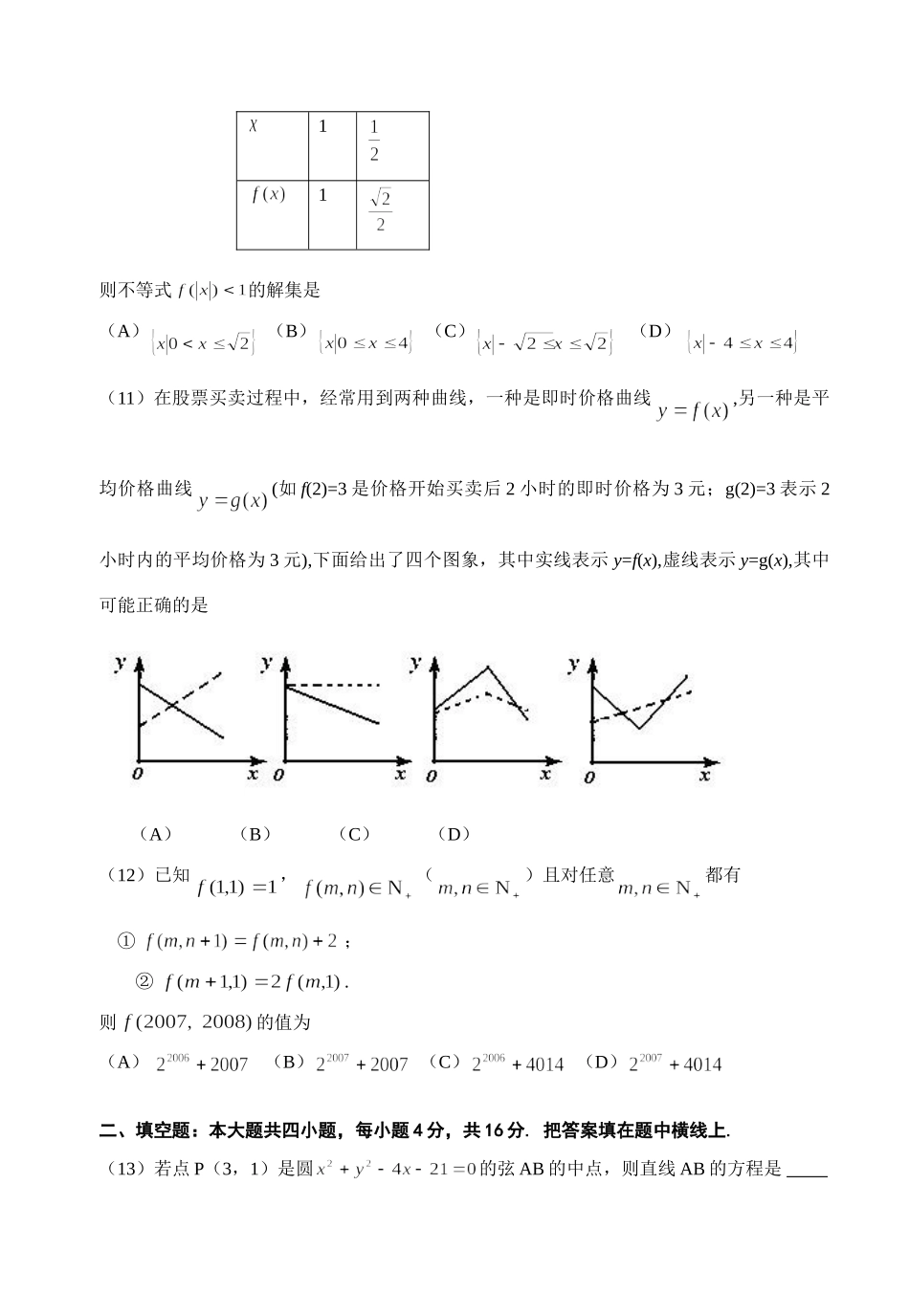
山东省潍坊市2007年高三第二次统一考试数学试题(理工农医类)2007.4第I卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出得四个选项中,只有一项是符合题目要求的.(1)的共轭复数是(A)-(B)(C)(D)(2)已知条件P:,条件:,则是的(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既非充分也非必要条件(3)一个几何体的三视图如图所示,则该几何体的体积等于(A)(B)(C)(D)(4)设某种动物由出生算起活到10岁的概率为0.9,活到15岁的概率为0.6.现有一个10岁的这种动物,它能活到15岁的概率是(A)(B)(C)(D)(5)设F是椭圆的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,则椭圆上与点F的距离是的点的坐标是(A)(0,(B)(C)(D)(6)已知,则的值是(A)(B)(C)24(D)12(7)如图,程序框图所进行的求和运算是(A)(B)(C)(D)(8)设双曲线的两条渐近线与直线围成的三角形区域(包含边界)为D,P()为D内的一个动点,则目标函数的最小值为(A)(B)(C)0(D)(9)设、、为平面,为直线,给出下列条件①;②;③;④其中能使成立的条件是(A)①②(B)②③(C)②④(D)③④(10)已知幂函数的部分对应值如下表:11则不等式的解集是(A)(B)(C)(D)(11)在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线,另一种是平均价格曲线(如f(2)=3是价格开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元),下面给出了四个图象,其中实线表示y=f(x),虚线表示y=g(x),其中可能正确的是(A)(B)(C)(D)(12)已知,()且对任意都有①;②.则的值为(A)(B)(C)(D)二、填空题:本大题共四小题,每小题4分,共16分.把答案填在题中横线上.(13)若点P(3,1)是圆的弦AB的中点,则直线AB的方程是.(14)在代数式的展开式中,常数项的是.(15)在样本的频率分布直方图中,共有4个小长方形,这4个小长方形的面积由小到大构成等差数列,已知,且样本容量为400,则小长方形面积最大的一组的频数为.(16)对于函数给出下列四个命题:①该函数是以为最小正周期的周期函数;②当且仅当时,该函数取得最小值是-1;③该函数的图象关于对称;④当且仅当时,其中正确命题的序号是(请将所有正确命题的序号都添上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12分)在ABC中,、、分别是A、B、C的对边.若向量m=(2,0)与n=()所成角为(I)求角B的大小;(II)若,求的最大值.(18)(本小题满分12分)已知数列的前项n和为,对一切正整数n,点(n,)都在函数的图象上.(I)求数列的通项公式;(II)设,求数列的前n项的和(19)(本小题满分12分)如图1,在直角梯形ABCP中,AP//BC,AP⊥AB,AB=BC=AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将PCD沿CD折起,使点P在平面ABCD上的射影为点D,如图2.(I)求证:AP//平面EFG;(II)求二面角E-FG-D的一个三角函数值.(20)(本小题满分12分)某次象棋比赛的决赛在甲乙两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分;比赛共进行五局,积分有超过5分者比赛结束,否则继续进行.根据以往经验,每局甲赢的概率为,乙赢的概率为,且每局比赛输赢互不受影响.若甲第n局赢、平、输的得分分别记为、、令.(Ⅰ)求的概率;(Ⅱ)若随机变量满足(表示局数),求的分布列和数学期望.(21)(本小题满分12分)如图,已知直线与抛物线相切于点P(2,1),且与轴交于点A,定点B的坐标为(2,0).(I)若动点M满足,求点M的轨迹C;(II)若过点B的直线(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求OBE与OBF面积之比的取值范围.(22)(本小题满分14分)设,其中,且(为自然对数的底数)(I)求与的关系;(II)若在其定义域内为单调函数,求的取值范围;(III)证明:①;②.山东省潍坊市2007年高三第二次统一考试数学试题(理工农医类)参考答案及评分标准2007.4一、选择题:每小题5分,共60分.BBACBACBCDCC二、填空题:每小题4分,共16分.(13)(14)-23(15)160...