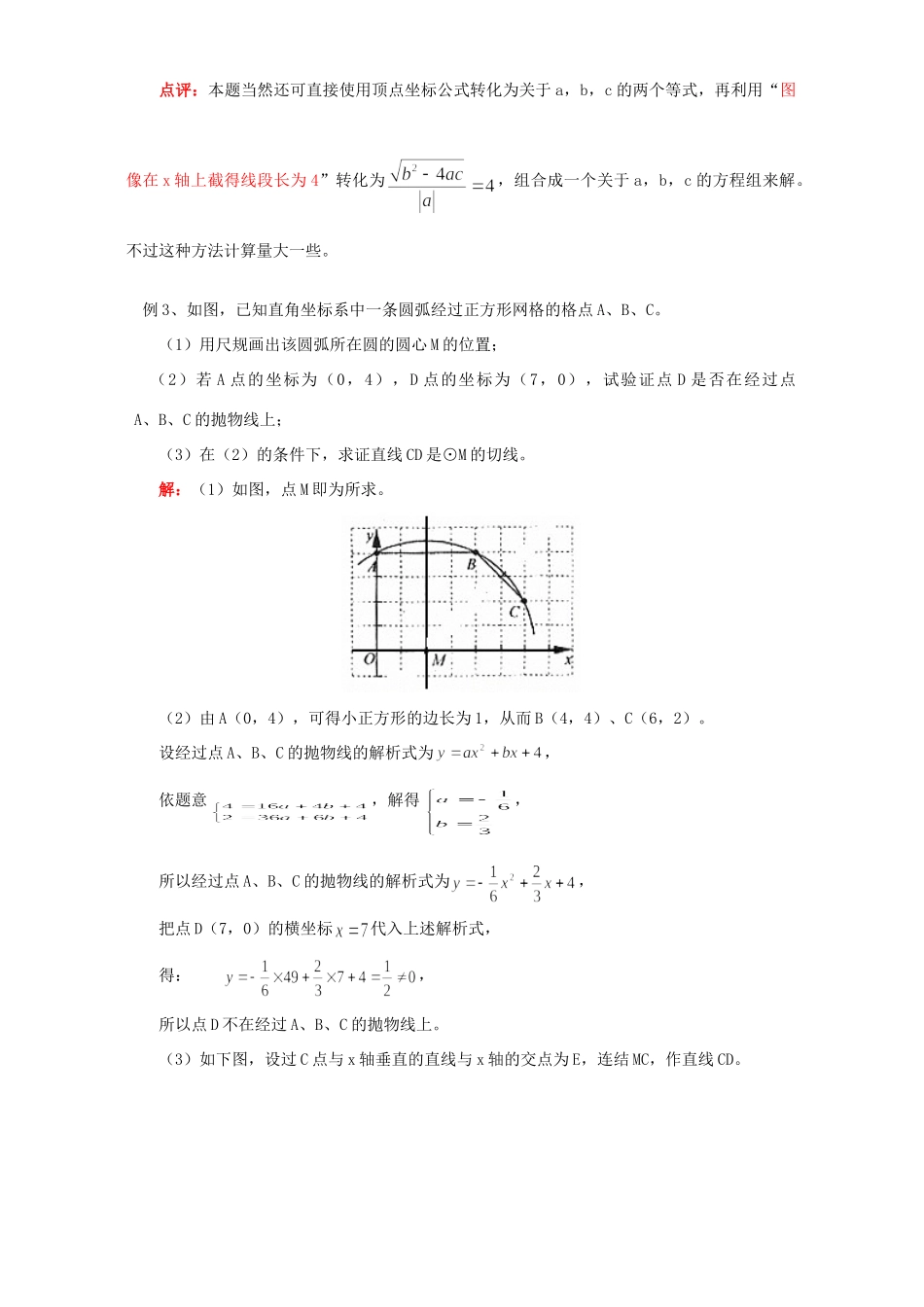
初三数学二次函数与一元二次方程实际问题与二次函数知识精讲一.本周教学内容:1.二次函数与一元二次方程2.实际问题与二次函数二、重、难点:二次函数解析式的确定和二次函数的应用抛物线的解析式有三种形式:①一般式:(a≠0);②顶点式:,(h,k)是顶点坐标;③交点式:(a≠0),其中x1,x2是方程的两个实根。在实际应用中,需要根据题目的条件选择相应的形式以简化计算。利用待定系数法确定二次函数的解析式的步骤可以总结为五个字:设、列、求、定。例1、已知二次函数图像顶点坐标为(-2,3),且过点(1,0),求此二次函数的解析式。(试用两种不同的方法)分析:根据所给条件中有顶点坐标的特点,可以选用顶点式。解法一:设二次函数的解析式为:因为二次函数图像过点(1,0)所以所以所以函数解析式为。分析:根据所给条件中顶点坐标可知,抛物线的对称轴为x=-2,利用抛物线的对称性,可求得点(1,0)关于对称轴x=-2的对称点(-5,0),可选用交点式。解法二:设二次函数的解析式为:,因为二次函数图像过点(-2,3)所以所以函数解析式为。点评:当题目条件中有顶点坐标时,选用顶点式;当条件中有两个与x轴的交点时,一般选用交点式。但我们注意到,解法二是在知道抛物线与x轴的一个交点后,利用对称轴可从顶点坐标中得到,再利用抛物线的对称性获得另外一个与x轴的交点坐标,再利用交点式获得结果。两种方法各有千秋,仔细体会必定会有所收获。当然此题也可使用一般式,但不如这两种方法简单。例2、已知二次函数,当x=-1时有最小值-4,且图像在x轴上截得线段长为4,求函数解析式。分析:当题目条件中点的条件不足三个时,要充分利用二次函数的对称性转化条件。在本题中由于所给条件能得到一个顶点坐标(-1,-4),另外一个条件是图像在x轴上截得的线段长,条件似乎不是特别充分。仔细分析,有“当x=-1时有最小值-4”就知道对称轴,再有“图像在x轴上截得线段长为4”,利用对称性可得图像与x轴的交点坐标为(-3,0),(1,0),从而可利用交点式解决问题。解: 当x=-1时有最小值-4,且图像在x轴上截得线段长为4∴函数图像与x轴交于(-3,0),(1,0)两点。∴设二次函数的解析式为 二次函数过(-1,-4)∴∴a=1∴点评:本题当然还可直接使用顶点坐标公式转化为关于a,b,c的两个等式,再利用“图像在x轴上截得线段长为4”转化为,组合成一个关于a,b,c的方程组来解。不过这种方法计算量大一些。例3、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。(1)用尺规画出该圆弧所在圆的圆心M的位置;(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A、B、C的抛物线上;(3)在(2)的条件下,求证直线CD是⊙M的切线。解:(1)如图,点M即为所求。(2)由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2)。设经过点A、B、C的抛物线的解析式为,依题意,解得,所以经过点A、B、C的抛物线的解析式为,把点D(7,0)的横坐标代入上述解析式,得:,所以点D不在经过A、B、C的抛物线上。(3)如下图,设过C点与x轴垂直的直线与x轴的交点为E,连结MC,作直线CD。所以CE=2,ME=4,ED=1,MD=5,在Rt△CEM中,∠CEM=90°,所以,在Rt△CED中,∠CED=90°,所以,所以,所以∠MCD=90°,因为MC为半径,所以直线CD是⊙M的切线。点评:本题第(1)问是一个尺规作图题,需要确定圆心的位置;第(2)问中所给三个点的坐标不具有使用顶点式和交点式的特点,所以只能踏踏实实地利用一般式求解;第(3)问和圆的知识结合起来,求证直线与圆相切。要求熟练使用线段与坐标的相互转化,在证明线与线的垂直关系时还需要使用勾股定理的逆定理。例4、已知抛物线与轴交于点,与轴分别交于,两点.(1)求此抛物线的解析式;(2)若点为线段的一个三等分点,求直线的解析式;(3)若一个动点自的中点出发,先到达轴上的某点(设为点),再到达抛物线的对称轴上某点(设为点),最后运动到点.求使点运动的总路径最短的点,点的坐标,并求出这个最短总路径的长.解:(1)根据题意,,所以解得所以抛物线解...