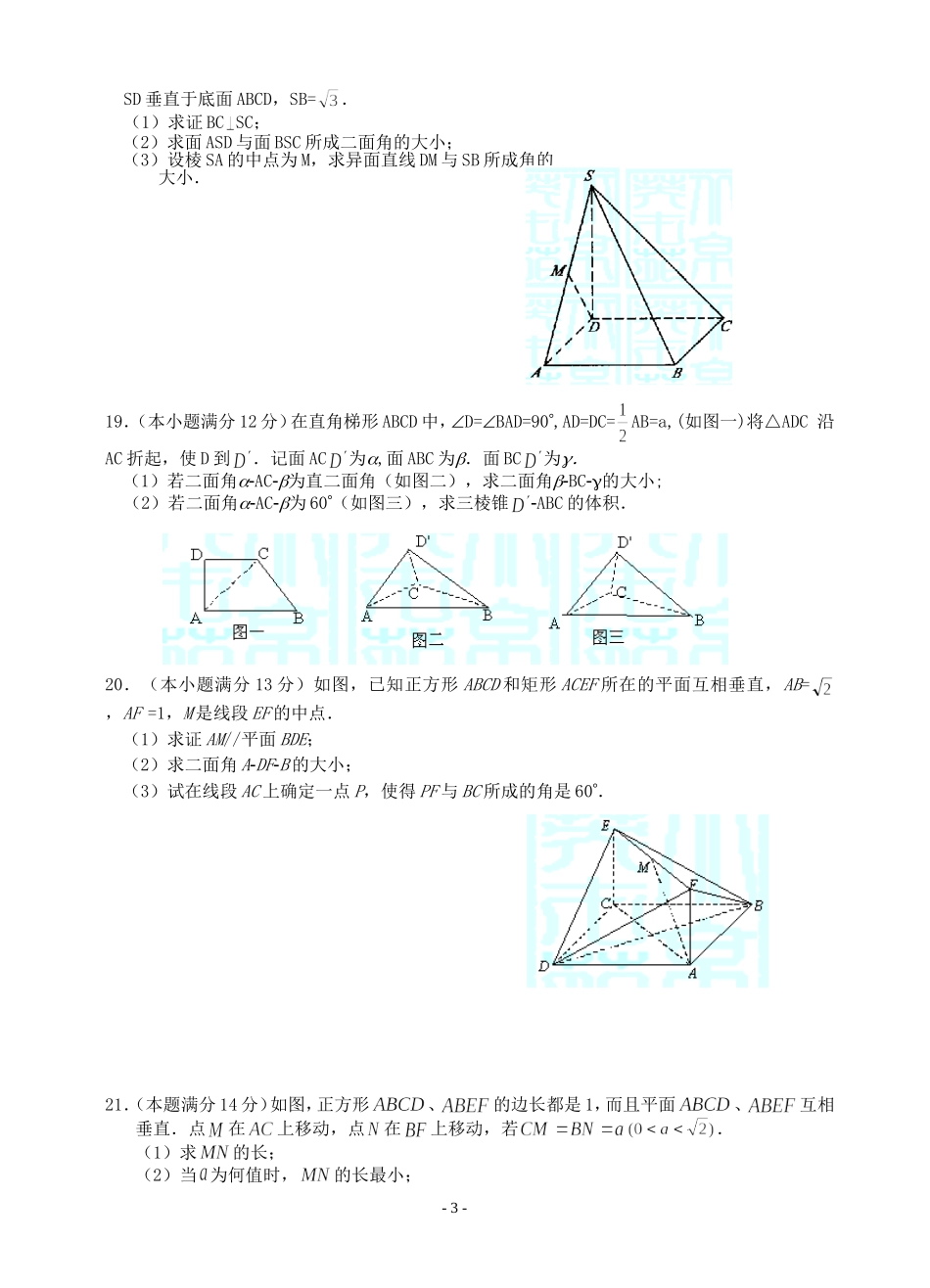
湖北省荆门市实验高中高二数学空间角和距离单元测试题一、选择题(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线m与平面间距离为d,那么到m与距离都等于2d的点的集合是()A.一个平面B.一条直线C.两条直线D.空集2.异面直线a、b所成的角为,a、b与平面都平行,b平面,则直线a与平面所成的角()A.与相等B.与互余C.与互补D.与不能相等.3.在正方体ABCD—ABCD中,BC与截面BBDD所成的角为()A.B.C.D.arctan24.已知点,,它们在面内的射影分别是,则()A.5B.6C.7D.85.有一山坡,它的倾斜角为30°,山坡上有一条小路与斜坡底线成45°角,某人沿这条小路向上走了200米,则他升高了()A.100米B.50米C.25米D.50米6.已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小为()A.arccosB.arccosC.D.7.正四面体A—BCD中E、F分别是棱BC和AD之中点,则EF和AB所成的角()A.45B.60C.90D.308.把∠A=60°,边长为a的菱形ABCD沿对角线BD折成60°的二面角,则AC与BD的距离为()A.aB.aC.aD.a9.若正三棱锥的侧面均为直角三角形,侧面与底面所成的角为α,则下列各等式中成立的是()A.0<α<B.<α<C.<α<D.<α<10.已知A(1,1,1),B(-1,0,4),C(2,-2,3),则〈,〉的大小为()A.B.C.D.二、填空题(本大题共5小题,每小题5分,共25分)11.从平面外一点P引斜线段PA和PB,它们与分别成45和30角,则APB的最大值是______最小值是_______12.ABC中ACB=90,PA平面ABC,PA=2,AC=2,则平面PBC与平面PAC,平面ABC所成的二角的大小分别是______、_________.-1-13.在三棱锥P-ABC中,,,BC=5,又PA=PB=PC=AC,则点P到平面ABC的距离是.14.长方体中,AB=4,BC=3,BB1=2,那么AD与平面的距离为________.15.如图,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,斜边AB=a,侧棱AA1=2a,点D是AA1的中点,那么截面DBC与底面ABC所成二面角的大小是________.三、解答题(共计75分)16.(本小题满分12分)已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.(1)求证:SC⊥面BDE;(2)求二面角E—BD—C的大小.17.(本小题满分12分)如图,点为斜三棱柱的侧棱上一点,交于点,交于点.(1)求证:;(2)在任意中有余弦定理:.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.18.(本小题满分12分)如图,四棱锥S—ABCD的底面是边长为1的正方形,-2-ABCDABC111SD垂直于底面ABCD,SB=.(1)求证BCSC;(2)求面ASD与面BSC所成二面角的大小;(3)设棱SA的中点为M,求异面直线DM与SB所成角的大小.19.(本小题满分12分)在直角梯形ABCD中,D=BAD=90,AD=DC=AB=a,(如图一)将△ADC沿AC折起,使D到.记面AC为,面ABC为.面BC为.(1)若二面角AC为直二面角(如图二),求二面角BC的大小;(2)若二面角AC为60(如图三),求三棱锥ABC的体积.20.(本小题满分13分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点.(1)求证AM//平面BDE;(2)求二面角ADFB的大小;(3)试在线段AC上确定一点P,使得PF与BC所成的角是60.21.(本题满分14分)如图,正方形、的边长都是1,而且平面、互相垂直.点在上移动,点在上移动,若.(1)求的长;(2)当为何值时,的长最小;-3-(3)当长最小时,求面与面所成的二面角的大小.-4-[参考答案]http://www.DearEDU.com一.选择题(本大题共10小题,每小题5分,共50分)题号12345678910答案CBCABCAACD二.填空题(本大题共4小题,每小题6分,共24分)11.1050,15012.900,30013.14.15.450三、解答题(本大题共6题,共76分)16.(12分)(1)证明:(1) SB=BCE是SC的中点∴BE⊥SC DE⊥SC∴SC⊥面BDE(2)解:由(1)SC⊥BD SA⊥...