高中数学 313空间向量的数量积课件 新人教B版选修2-1 课件VIP免费

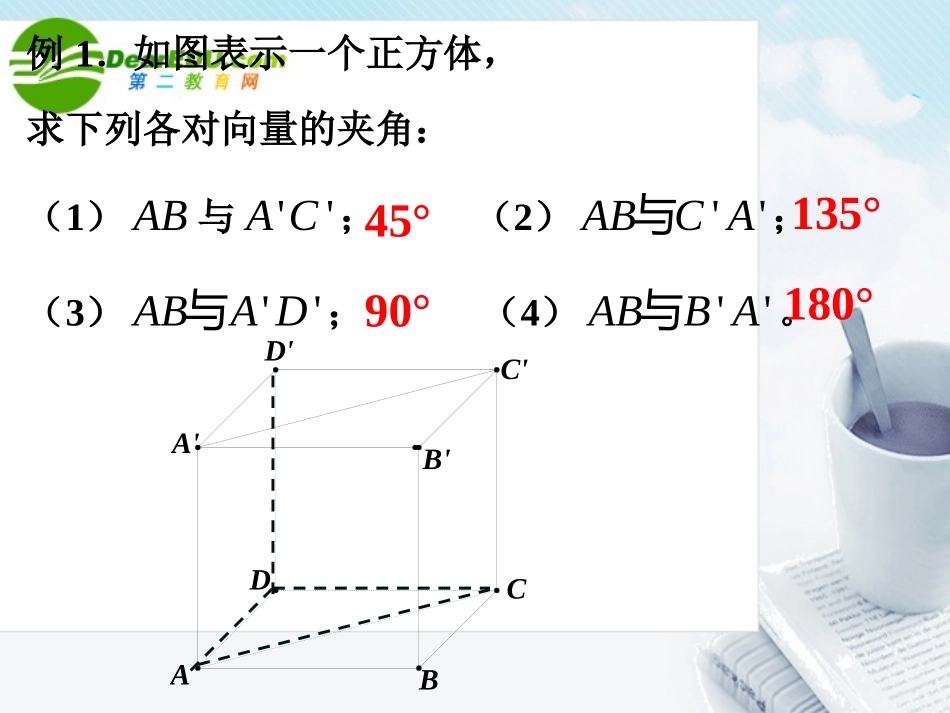
3.1.3空间向量的数量积1．空间向量的夹角及其表示：已知两非零向量,ab，在空间任取一点O，作,OAaOBb�，则AOB叫做向量a与b的夹角，记作,ab；且规定0,ab，显然有,,abba；若,2ab，则称a与b互相垂直，记作：ab；例1．如图表示一个正方体，求下列各对向量的夹角：（1）AB�与''AC�；（2）''ABCA�与；（3）''ABAD�与；（4）''ABBA�与。45°135°90°180°D'C'B'A'DBAC2．向量的模：设OAa�，则有向线段OA�的长度叫做向量a的长度或模，记作：||a；3．向量的数量积：已知向量,ab，则||||cos,abab叫做,ab的数量积，记作ab，即ab||||cos,abab．4．空间向量数量积的性质：(1)||cos,aeaae(2)0abab2(3)||aaa(4)||||||abab≤5．空间向量数量积运算律：(1)()()()ababab(2)abba(3)()abcabac下面我们来证明数量积的分配律。已知向量a，b，c，如果这三个已知向量共面，在平面向量中我们已经证明分配律成立。现在假设这三个向量不共面。作//lc，设轴的单位向量为0c�，c0baclB'A'BAO在l上取O点作OAa�，作ABb�，连OB，则OBab�，过点A作AA’垂直l于点A’，过点B作BB’垂直l于点B’，则00()'abcOBcOB��，00'acOAcOA��，00''bcABcAB��，因为OB’=OA’+A’B’，所以000()abcacbc��，上式两边同乘以||c，即可证明()abcacbc。例2．用向量方法证明：直线和平面垂直的判定定理。已知：m，n是平面α内的两条相交直线，直线l与平面α的交点为B，且l⊥m，l⊥n求证：l⊥α．lmnmnggl证明：在内作不与,mn重合的任一直线g，在,,,lmng上取非零向量,,,lmng， ,mn相交，∴向量,mn不平行，由共面定理可知，存在唯一有序实数对(,)xy，使gxmyn，∴lgxlmyln，又 0,0lmln，∴0lg，∴lg，∴lg，所以，直线l垂直于平面内的任意一条直线，即得l．例3．已知空间四边形ABCD中，AB⊥CD,AC⊥BD，求证：AD⊥BC．证明：()()ADBCABBDACAB�2ABACBDACABABBD�()0ABACABBDABDC�．证二：选取一组基底，设,,ABaACbADc�， ABCD，∴()0acb，即acba，同理：abbc，，∴acbc，∴()0cba，∴0ADBC�，即ADBC．例4．已知平面α⊥平面β，α∩β=l，点A、B在α内，并且它们在l上的正射影分别为A’，B’；C，D在β内，并且它们在l上的正射影分别为C’，D’，求证：''''ABCDABCD�D'DC'ClB'A'BA证明：因为A’B’和C’D’分别为AB和CD在l上的正射影，又因为αβ⊥，所以AA’//BB’，并且它们都与CC’，CD，DD’垂直，CC’//DD’，并且它们都与AA’，A’B’，BB’垂直。因此，','AABB�分别和','','CCCDDD�的数量积等于零；','CCDD�分别和','','AAABBB�的数量积等于零；从而可得('''')('''')''''ABCDAAABBBCCCDDDABCD���例5．已知长方体ABCD－A’B’C’D’，AB=AA’=2，AD=4，E为侧面AB’的中心,F为A’D’的中点，计算下列数量积：'BCED�'BFAB�'EFFC�1602FED'DC'CbacB'A'BA1、下列命题：①若0ab，则a，b中至少一个为0；②②若a0且abac，则bc③()()abcabc；④22(32)(32)94ababab,其中正确有个数为（）A.0个B.1个C.2个D.3个B练习题2、已知△ABC中，A，B，C所对的边为a,b,c，且a=3,b=1,C=30°,则=。BCCA�3323、若a，b，c满足0abc，且3,1,4abc，则abbcac=。－134、已知2ab，且a与b的夹角为3，则ab在a上的投影为...