高中数学 点的轨迹与几何不等式课件 苏教版必修5 课件VIP免费

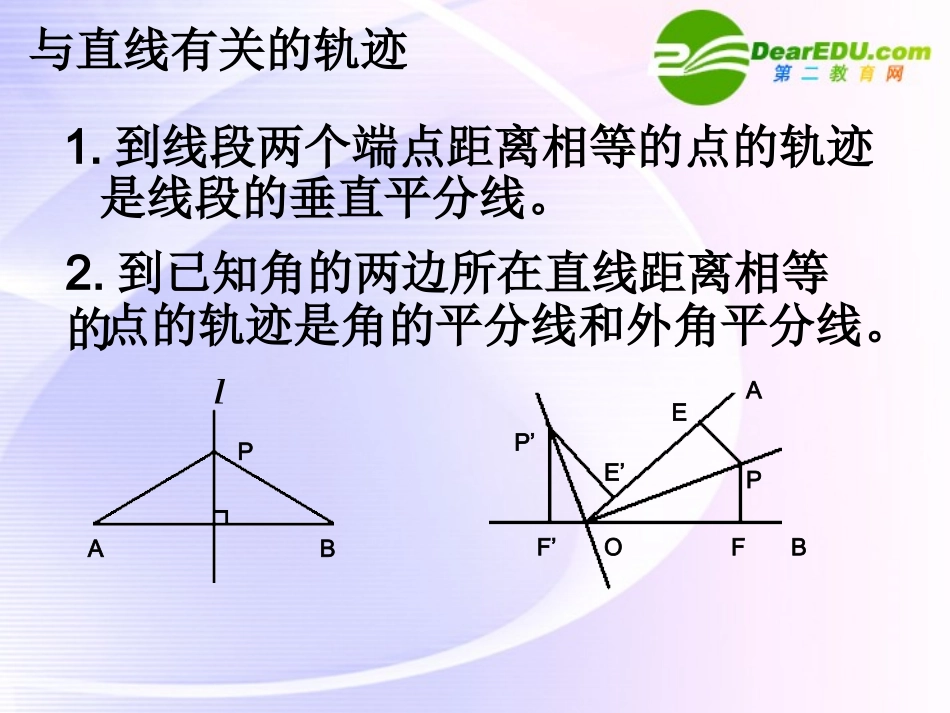
点的轨迹与几何不等式网络同步助学——第十五讲与直线有关的轨迹1.到线段两个端点距离相等的点的轨迹是线段的垂直平分线。lABPF’P’FBEAPE’O2.到已知角的两边所在直线距离相等的点的轨迹是角的平分线和外角平分线。3.到已知直线距离等于定值的点的轨迹是与已知直线平行，并且到这条直线距离等于定值的两条平行直线。与直线有关的轨迹4.到两条平行直线距离相等的点的轨迹是和这两条平行直线平行且距离相等的一条直线。O例1.已知梯形ABCD（如图），画一条圆弧与两腰连接，并且在连接点与两腰所在直线相切。例题讲解1BADC作法：延长DA，CB相交于O，作∠DOC的平分线，在角平分线适当位置取圆心P，以P到AD距离为半径作弧。（圆弧不唯一）解:因为圆弧与两腰相切,所以圆心到两腰距离相等,圆心在两腰所成角的平分线上。P例题讲解2例2:已知⊙O中弦，若圆上恰有3个点到AB的距离等于1，求该圆的半径.32AB分析:到直线AB距离为1的点的轨迹是与AB平行且到AB距离为1的两平行线。又因为圆上恰有3个点到AB的距离等于1,所以两条平行线中恰有一条与圆相切,不妨设与圆O相切于点C。1lC例2.已知⊙O中弦，若圆上恰有3个点到的距离等于1，求该圆的半径.32AB解:取AB中点M,连接OA,OC，则OC经过M，设圆半径为R。222OMAMAO2223(1)RR2R答:该圆半径为2。例题讲解1C与圆有关的轨迹1.到定点的距离等于定长的点的轨迹是以定点为圆心以定长为半径的圆。POrPAB2.对两个定点的张角为直角的点的轨迹是以这两个定点连线为直径的圆。（除两个定点）3.对两个定点的张角为定角（不是直角）的点的轨迹为二段圆弧（除两个端点）与圆有关的轨迹PP’ABABPP’例3.如图，点P在⊙O外，⊙O的半径为2，点Q在⊙O上运动，线段PQ，OP的中点分别为A，B,求点A的轨迹.例题讲解3OQP∴ABOQ12解:∵线段PQ，OP的中点分别为A，B∴AB=1∴点A的轨迹是以B为圆心，半径为1的圆BA点与直线的几何不等式1.两点之间线段最短2.三角形两边之和大于第三边，第三边大于两边之差3.直角三角形的斜边大于直角边（连结直线外一点和直线上一点的所有线段中，垂线段最短）点与圆的几何不等式设⊙C的半径r,点P不在圆上，PC=d,PC交⊙C于A，B两点（A点靠近P），则PA为圆周上的点到P点的最短距离，PB为圆周上的点到P点的最长距离,且PA=|d-r|PCAACPBB例题讲解4例4.(1)已知A,B在直线的同侧,在上找一点P,使PA+PB最小.ll解:作A关于的对称点A’,连结A’B,交于P,则P为所求点llA’PBAl例题讲解4例4.(2)如图,已知A,B在直线的异侧,在上找一点P,使PA-PB最大.ll解:作A关于的对称点A’,连结A’B,并延长交于P,则P为所求PA-PB最大值为|A’B|llAA’PBP’l例5.如图：已知CD是Rt△ABC斜边AB上的高求证:AB+CD>AC+BC.ͼ1-41FEDCBA解:因为AC>CD,在AC上截取CE=CD,过E作EF∥CB交AB于F,连接CF显然RtCFERtCFD△≌△∴∠CFD=CFE=BCF∠∠∴BC=BF又AF>AE∴AB+CD=AF+BF+CD>AE+BC+CD=AE+CE+BC=AC+BC例题讲解5再见!