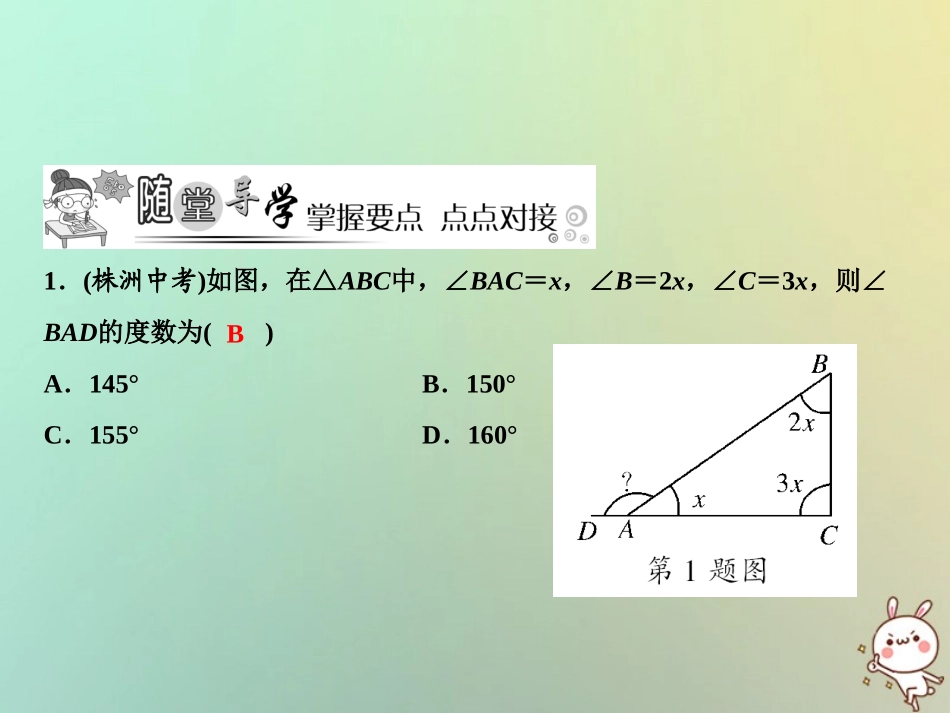
第13章三角形中的边角关系、命题与证明13.1三角形中的边角关系第2课时2018秋季数学八年级上册•HK三角形按角分类自我诊断1.三角形按角分类的标准是的大小.自我诊断2.若三角形的三个内角∠A∶∠B∶∠C=1∶2∶3,则△ABC是三角形.三角形的内角和自我诊断3.锐角三角形中,最大角α的取值范围是()A.0°<α<90°B.60°<α<180°C.60°<α<90°D.60°≤α<90°最大角直角D1.(株洲中考)如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD的度数为()A.145°B.150°C.155°D.160°B2.(新疆中考)如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC的度数为()A.20°B.50°C.80°D.100°C3.(凉山中考)如图,AB∥CD,则下列式子一定成立的是()A.∠1=∠3B.∠2=∠3C.∠1=∠2+∠3D.∠3=∠1+∠2D4.如图是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,则这块三角形木板另外一个角是度.405.判断适合下列条件的△ABC是锐角三角形、钝角三角形还是直角三角形.(1)∠A=80°,∠B=25°;(2)∠A-∠B=30°,∠B-∠C=36°;(3)∠A=12∠B=16∠C.(2)设∠B=x°,则∠A=(30+x)°,∠C=(x-36)°,所以x°+(30+x)°+(x-36)°=180°,解得x=62.所以最大角∠A=92°,所以△ABC是钝角三角形;(3)设∠A=x°,∠B=2x°,∠C=6x°,则x°+2x°+6x°=180°,解得x=20.所以∠C=120°,所以△ABC是钝角三角形.解:(1)因为在△ABC中,∠A+∠B+∠C=180°(三角形的三个内角和等于180°),∠A=80°,∠B=25°,所以∠C=180°-80°-25°=75°.所以△ABC是锐角三角形;6.(乐山中考)含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2,∠ACD=∠A,则∠1的度数为()A.70°B.60°C.40°D.30°B7.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于()A.40°B.60°C.80°D.90°8.如图,C在AB的延长线上,CE⊥AF交AF于点E,交BF于点D.∠F=40°,∠C=20°,则∠FBA的度数为()A.50°B.60°C.70°D.80°AC9.在下列条件中:①∠A+∠B=∠C;②∠A∶∠B∶∠C=2∶3∶4;③∠A=90°-∠B;④∠A=∠B=12∠C.能确定△ABC是Rt△ABC的条件有()A.1个B.2个C.3个D.4个10.在△ABC中,三个内角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B=.C60°11.(泰州中考)将一副三角尺如图叠放,则图中∠α的度数为.12.一副三角板如图所示叠放在一起,则图中∠α的度数是.15°75°13.如图所示,∠1+∠2+∠3+∠4+∠5+∠6=.360°14.如图,AB∥CD,AD、BC相交于点O.若∠B=20°,∠1=110°,求∠D的度数.解:在△AOB中,因为∠B=20°,∠1=110°,所以∠A=180°-20°-110°=50°.因为AB∥CD,所以∠A=∠D,所以∠D=50°.15.(郴州中考)小明把一副含45°、30°的直角三角尺按如图所示的方式摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,求∠α+∠β的值.解:∠α+∠β=210°.16.(1)如图①,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两直角边XY、XZ分别经过点B、C.在△ABC中,∠A=30°,则∠ABC+∠ACB=,∠XBC+∠XCB=;(2)如图②,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.150°90°解:(2)不变化.∵∠A=30°,∴∠ABC+∠ACB=150°,∵∠X=90°,∴∠XBC+∠XCB=90°,∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=60°.