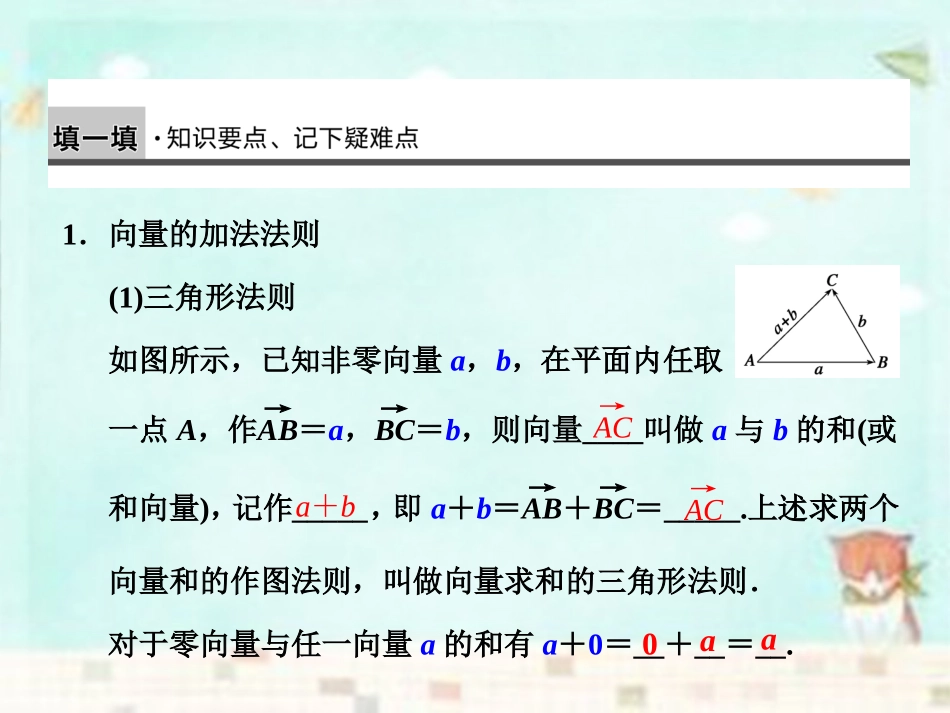
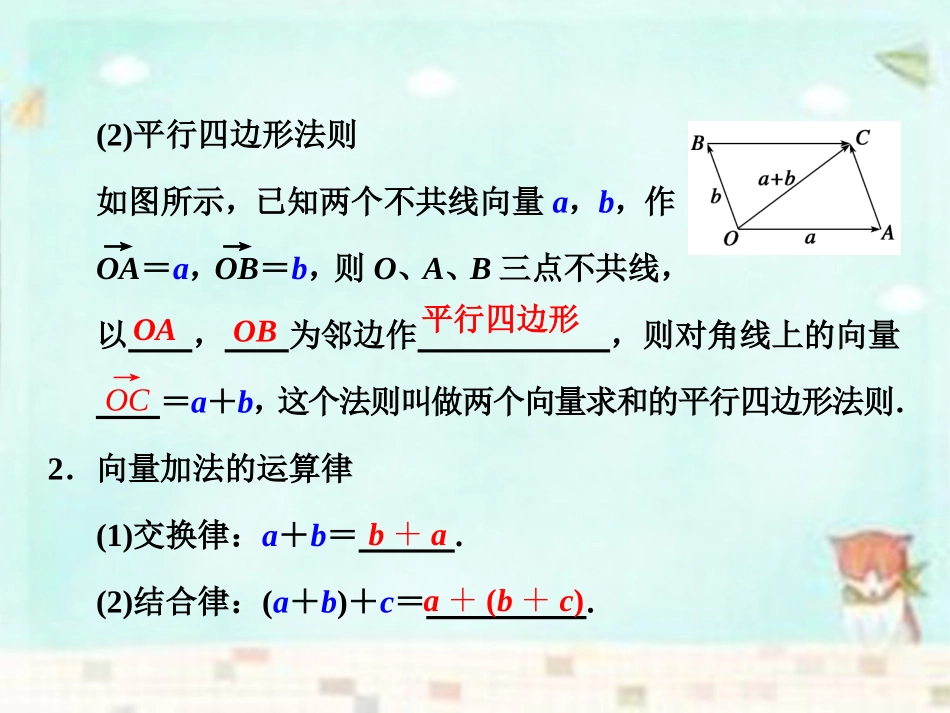
1.向量的加法法则(1)三角形法则如图所示,已知非零向量a,b,在平面内任取一点A,作AB→=a,BC→=b,则向量____叫做a与b的和(或和向量),记作_____,即a+b=AB→+BC→=_____.上述求两个向量和的作图法则,叫做向量求和的三角形法则.对于零向量与任一向量a的和有a+0=__+__=__.AC→a+bAC→0aa(2)平行四边形法则如图所示,已知两个不共线向量a,b,作OA→=a,OB→=b,则O、A、B三点不共线,以,为邻边作,则对角线上的向量=a+b,这个法则叫做两个向量求和的平行四边形法则.2.向量加法的运算律(1)交换律:a+b=.(2)结合律:(a+b)+c=.OAOB平行四边形OC→b+aa+(b+c)探究点一向量加法的三角形法则如图所示,是上海到台北的航线示意图:一是经香港转停到台北;二是由上海直接飞往台北.通过上面地图中客机的位移,我们得到向量加法的三角形法则:OA→+AB→=OB→.使用向量加法的三角形法则具体做法是:先把两个向量首尾顺次相接,然后连接第一个向量的始点和后一个向量的终点,并指向后一个向量的终点,就得到两个向量的和向量.问题1当向量a,b是共线向量时,a+b又如何作出?答(1)当a与b同向时:OB→=OA→+AB→=a+b(2)当a与b反向时:OA→=a,AB→=b,OB→=OA→+AB→=a+b.问题2想一想,|a+b|与|a|和|b|之间的大小关系如何?当a与b同向共线时,a+b与____同向,且|a+b|=_______.当a与b反向共线时,若|a|>|b|,则a+b与__的方向相同,且|a+b|=_______;若|a|<|b|,则a+b与__的方向相同,且|a+b|=_______.|a|+|b||a|-|b||b|-|a|a,bab探究点二向量加法的平行四边形法则向量加法还可以用平行四边形法则:先把两个已知向量的起点平移到同一点,再以这两个已知向量为邻边作平行四边形,则这两邻边所夹的对角线就是这两个已知向量的和.以点A为起点作向量AB→=a,AD→=b,以AB、AD为邻边作▱ABCD,则以A为起点的对角线AC→就是a与b的和,记作a+b=AC→,如图.对于零向量与任一向量a,我们规定:a+0=0+a=a.①根据下图中的平行四边形ABCD验证向量加法的交换律:a+b=b+a.(注:AB→=a,AD→=b).答 AC→=AB→+BC→,∴AC→=a+b. AC→=AD→+DC→,∴AC→=b+a.∴a+b=b+a.②根据下图中的四边形,验证向量加法的结合律:(a+b)+c=a+(b+c).答 AD→=AC→+CD→=(AB→+BC→)+CD→,∴AD→=(a+b)+c,又 AD→=AB→+BD→=AB→+(BC→+CD→),∴AD→=a+(b+c),∴(a+b)+c=a+(b+c).探究点三向量加法的多边形法则向量加法的三角形法则可以推广为多个向量求和的多边形法则,即把每个向量平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向量就是这些向量的和向量.即:A1A2→+A2A3→+A3A4→+…+An-1An=A1An→.或A1A2→+A2A3→+…+An-1An+AnA1→=__.这是一个极其简单却非常有用的结论(如图).0利用向量加法的多边形法则化简多个向量的和有时非常有效.例如,在正六边形ABCDEF中,AC→+BD→+CE→+DF→+EA→+FB→=________.解析AC→+BD→+CE→+DF→+EA→+FB→=(AB→+BC→)+(BC→+CD→)+(CD→+DE→)+(DE→+EF→)+(EF→+FA→)+(FA→+AB→)=(AB→+BC→+CD→+DE→+EF→+FA→)+(BC→+CD→+DE→+EF→+FA→+AB→)=0+0=0.0【典型例题】例1已知向量a,b如图所示,试用三角形法则和平行四边形法则作出向量a+b.解方法一三角形法则.(图1)在平面内任取一点O,作OA→=a,AB→=b,则OB→=a+b.图1图2方法二平行四边形法则.(图2)在平面内任取一点O,作OA→=a,OB→=b,以OA,OB为邻边作平行四边形,连接对角线OC,则OC→=OA→+OB→=a+b.小结已知向量a与b,要作出和向量a+b,关键是准确规范地依据三角形法则或平行四边形法则作图.跟踪训练1如图,已知向量a,b,c,利用三角形法则作出向量a+b+c.解在平面内任取一点O,作向量OA→=a,接着作向量AB→=c,则得向量OB→=a+c,然后作向量BC→=b,则向量OC→=a+b+c为所求和向量.例2化简:(1)BC→+AB→;(2)DB→+CD→+BC→;(3)AB→+DF→+CD→+BC→+FA→.解(1)BC→+AB→=AB→...