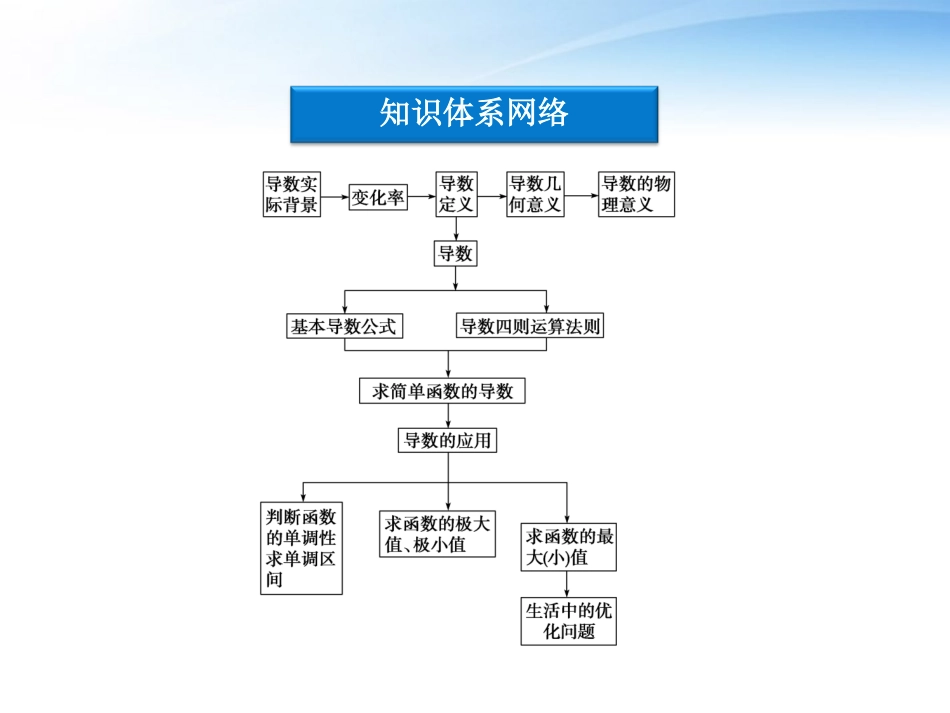
本章优化总结专题探究精讲本章优化总结知识体系网络知识体系网络专题探究精讲导数的几何意义题型特点:对导数的几何意义考查,最常见的问题就是求过曲线上某点的切线的斜率、方程、斜率与倾斜角的关系,以平行或垂直直线斜率间的关系为载体求参数的值,以及与曲线的切线相关的计算题.考查的题型以选择题、填空题为主.知识方法:函数y=f(x)在点x0处的导数的几何意义是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.也就是说,曲线y=f(x)在点P(x0,f(x0))处的切线的斜率为f′(x0),相应的切线方程为y-y0=f′(x0)(x-x0).已知函数f(x)=x3+x-16.(1)求曲线y=f(x)在点(2,-6)处的切线方程;(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;(3)如果曲线y=f(x)的某一切线与直线y=-14x+3垂直,求切点坐标与切线的方程.例例11【解】(1)可判定点(2,-6)在曲线y=f(x)上. f′(x)=(x3+x-16)′=3x2+1,∴f(x)在点(2,-6)处的切线的斜率为k=f′(2)=13.∴切线的方程为y=13(x-2)+(-6),即y=13x-32.(2)法一:设切点为(x0,y0),则直线l的斜率为f′(x0)=3x20+1,∴直线l的方程为y=(3x20+1)(x-x0)+x30+x0-16,又 直线l过点(0,0),∴0=(3x20+1)(-x0)+x30+x0-16,整理得,x30=-8,∴x0=-2.∴y0=(-2)3+(-2)-16=-26,k=3×(-2)2+1=13.∴直线l的方程为y=13x,切点坐标为(-2,-26).法二:设直线l的方程为y=kx,切点为(x0,y0),则k=y0-0x0-0=x30+x0-16x0,又 k=f′(x0)=3x20+1,∴x30+x0-16x0=3x20+1,解之得,x0=-2,∴y0=(-2)3+(-2)-16=-26,k=3×(-2)2+1=13.∴直线l的方程为y=13x,切点坐标为(-2,-26).(3) 切线与直线y=-x4+3垂直,∴切线的斜率k=4.设切点坐标为(x0,y0),则f′(x0)=3x20+1=4,∴x0=±1,∴x0=1y0=-14或x0=-1,y0=-18.即切点为(1,-14)或(-1,-18).切线方程为y=4(x-1)-14或y=4(x+1)-18.即y=4x-18或y=4x-14.题型特点:该题型主要考查求函数的单调区间、证明或判断函数的单调性,并经常与分类讨论,数形结合等思想方法的考查融为一体.在高考命题中,三种类型均有可能出现,若以选择题或填空题的形式出现,难度则以中低档为主,若以解答题形式出现,难度则以中等偏上为主.利用导数研究函数的单调区间知识方法:应用导数求函数的单调区间的步骤:(1)确定函数的定义域;(2)求导数f′(x);(3)解不等式f′(x)>0或f′(x)<0;(4)确定并指出函数的单调增区间、减区间.特别要注意写单调区间时,区间之间用“和”或“,”隔开,绝对不能用“∪”连结.设函数f(x)=1xlnx(x>0,且x≠1).求函数f(x)的单调区间.例例22【解】由题意知函数的定义域为(0,1),(1,+∞).f′(x)=-lnx+1x2ln2x.令f′(x)=0,则x=1e;令f′(x)>0,则0<x<1e;令f′(x)<0,则1e<x<1或x>1.故函数f(x)的单调递增区间是(0,1e);单调递减区间是(1e,1)和(1,+∞).题型特点:极值问题在高考中主要以解答题的形式出现,属中档题目,它作为工具性知识能解决诸如最值、不等式证明问题,随着对数学应用能力要求的加强,这方面的命题将有所增加.知识方法:1.应用导数求函数极值的一般步骤:(1)确定函数f(x)的定义域;(2)解方程f′(x)=0的根;(3)检验f′(x)=0的根的两侧f′(x)的符号.利用导数研究函数的极值和最值若左正右负,则f(x)在此根处取得极大值;若左负右正,则f(x)在此根处取得极小值;否则,此根不是f(x)的极值点.2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤:(1)求f(x)在(a,b)内的极值;(2)将(1)求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点处取得;②当f(x)在(a,b)内只有一个极值点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(或最小)值,这里(a,b)也可以是(-∞,+∞).已知函数f(x)=-x3+ax2+bx,在区间[-2,1]内,当x=-1时取极小值,当x=23时取极大值.(1)求函数y=...