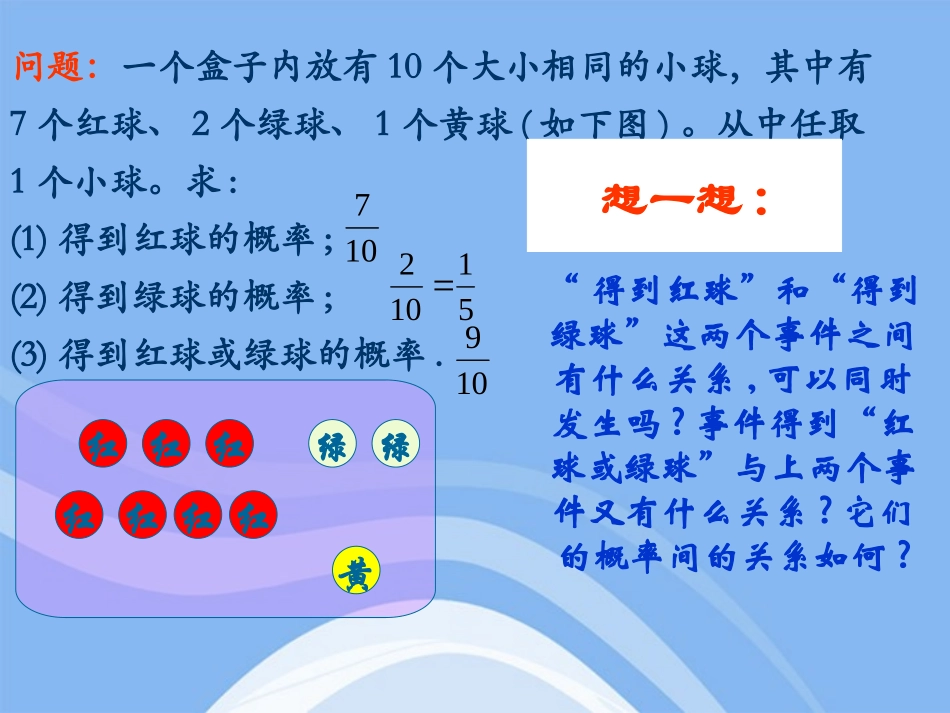
问题:一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、1个黄球(如下图)。从中任取1个小球。求:(1)得到红球的概率;(2)得到绿球的概率;(3)得到红球或绿球的概率.红绿黄绿红红红红红红10751102109“得到红球”和“得到绿球”这两个事件之间有什么关系,可以同时发生吗?事件得到“红球或绿球”与上两个事件又有什么关系?它们的概率间的关系如何?想一想:我们把“从中摸出1个球,得到红球”叫做事件A,“从中摸出1个球,得到绿球”叫做事件B,“从中摸出1个球,得到黄球”叫做事件C.红绿黄绿红红红红红红如果从盒中摸出的1个球是红球,即事件A发生,那么事件B就不发生;如果从盒中摸出的1个球是绿球,即事件B发生,那么事件A就不发生.就是说,事件A与B不可能同时发生.在一次试验中不可能同时发生的两个事件叫做互斥事件。11.互斥事件的定.互斥事件的定义义红绿绿红红红红红红C黄AB对于上面的事件A、B、C,其中任何两个都是互斥事件,这时我们说事件A、B、C彼此互斥.一般地,如果事件A1,A2,…,An中的任何两个都是互斥事件,那么就说事件A1,A2,…,An彼此互斥。从集合的角度看,几个事件彼此互斥,是指由各个事件所含的结果组成的集合彼此互不相交,如图所示。容易看到,事件B与C也是互斥事件,事件A与C也是互斥事件。判断以下各组中的事件是否是互斥事件?是否是等可能事件?练习:1.粉笔盒里有8支红粉笔,6支绿粉笔,4支黄粉笔,现从中任取1支,“抽得红粉笔”,“抽得绿粉笔”,“抽得黄粉笔”;2.李明从分别标有1,2,…,10标号的小球中,任取一球,“取的1号球”,“取的2号球”,…,“取的10号球”;是互斥事件,不是等可能事件是互斥事件,是等可能事件在上面的问题中,“从盒在上面的问题中,“从盒中摸出中摸出11个球,得到红球或绿个球,得到红球或绿球”是一个事件,当摸出的是球”是一个事件,当摸出的是红球或绿球时,表示这个事件红球或绿球时,表示这个事件发生,我们把这个事件记作发生,我们把这个事件记作AA++BB。。事件事件AA++BB的概率是的概率是多少多少答:答:P(AP(A++B)B)==P(A)P(A)++P(B)P(B)如果事件如果事件AA,,BB互斥,那么事件互斥,那么事件AA++BB发生发生((即即AA,,BB中有一个发生中有一个发生)的概率,等于事件)的概率,等于事件AA,,BB分别发生的概率的和分别发生的概率的和..22.互斥事件有一个发生的概率.互斥事件有一个发生的概率红绿绿红红红红红红C黄ABI一般地,如果事件一般地,如果事件AA11,,AA22,…,,…,AAnn彼此互彼此互斥,那么事件斥,那么事件AA11++AA22+…++…+AAnn发生(即发生(即AA11,,AA22,…,,…,AAnn中有一个发生)的概率,等于这中有一个发生)的概率,等于这nn个事件分别发生的概率的和,即个事件分别发生的概率的和,即PP((AA11++AA22+…++…+AAnn))=P(A=P(A11)+P(A)+P(A22)+…+P(A)+…+P(Ann))IAA由于事件A与不可能同时发生,它们是互斥事件。事件A与必有一个发生.这种其中必有一个发生互斥事件叫做对立事件对立事件.事件A的对立事件通常记作AA红红红红红红红A绿绿C黄B从集合的角度看,由事件所含的结果组成的集合,是全集I中的事件A所含的结果组成的集合的补集。AA33.对立事件.对立事件A从盒中摸出1个球,得到的不是红球(即绿球或黄球)”记作事件。AA必然事件由对立事件的意义概率为1互斥与AA)AP(A)AP(P(A)P(A)1)AP(44.对立事件的概率间的关系.对立事件的概率间的关系??:.,.,是否为对立事件是否为互斥事件与事件事件问件为事球只黑只白球和摸出事件记摸出两只白球为只球从中一次任意摸出黑球只与只白球的内装有大小一样一只口袋例BABA112441.互斥与事件解BA.,不是对立事件与所以事件只黑球因为从中一次可以摸出BA2判别下列每对事件是不是互斥事件,如果是,再判别它们是不是对立事件.从一堆产品(其中正品与次品都多于2个)中任取2件,其中:(1)恰有1件次品和恰有2件正品;(2)至少有1件次品和全是次品;(3)至少有1件正品和至少有1件次品;(4)至少有1件次品和全是正品;答案:(互斥但不对立,不互斥,不互斥,互斥...