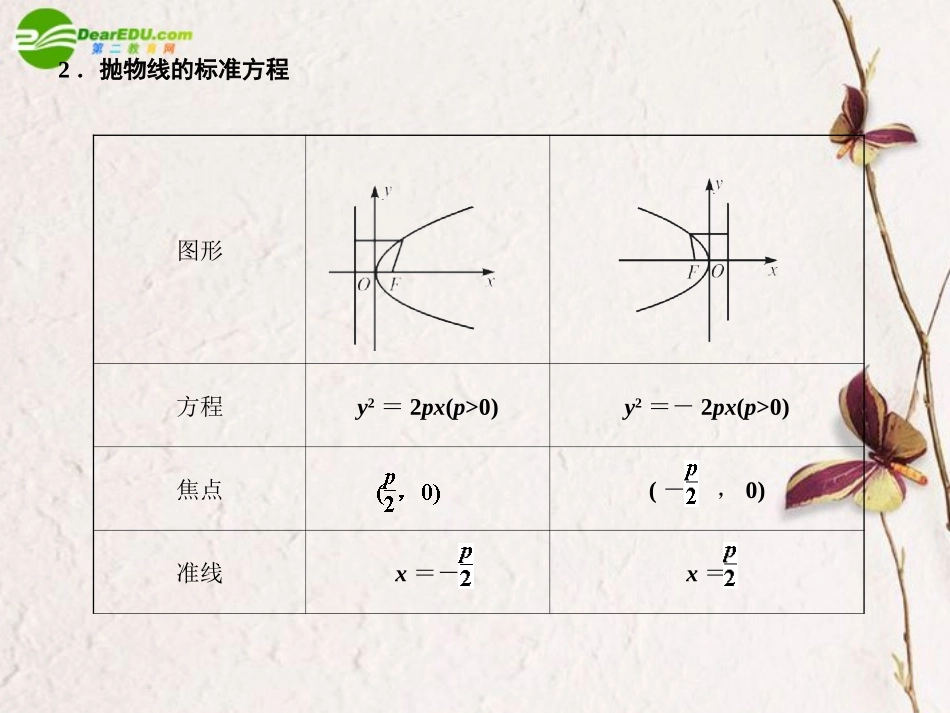
掌握抛物线的定义、标准方程第40课时抛物线的定义和标准方程1.抛物线定义平面内到一个定点F和一条定直线l(F∉l)的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的,定直线l叫做抛物线的.焦点准线图形方程y2=2px(p>0)y2=-2px(p>0)焦点(-,0)准线x=-x=2.抛物线的标准方程图形方程x2=2py(p>0)x2=-2py(p>0)焦点(0,)(0,-)准线y=-y=1.设F是抛物线E的焦点,经过F的直线与抛物线E交于P,Q两点,以PQ为直径的圆与抛物线E的准线的位置关系是()A.相交B.相离C.相切D.相交、相切、相离都有可能解析:过P、Q分别作抛物线准线的垂线,垂足分别为M、N,可知PF=PM,QF=QN,取PQ的中点O及MN中点H,可知OH=(PM+QN)=PQ,∴圆与其准线相切,∴选C.答案:C2.在抛物线y2=2px上,横坐标为4的点到焦点的距离为5,则p的值为()A.B.1C.2D.4解析:由抛物线定义可知:+4=5,∴p=2.答案:C3.过抛物线焦点F的直线与抛物线交于A、B两点,若A、B在抛物线准线上的射影分为A1、B1,则∠A1FB1等于()A.30°B.45°C.60°D.90°解析:如图所示,由定义知AA1=AF,BB1=BF,∴∠BB1F=∠BFB1,∠AA1F=∠AFA1,∠A1FB1=180°-(∠B1A1F+∠A1B1F),∴2∠A1FB1=180°,∴∠A1FB1=90°,此题可用特殊值法,即以AB垂直x轴时为例(详解略).答案:D4.抛物线y=ax2的准线方程是y=2,则a的值为()答案:B要注意点F不在直线l上,否则轨迹不是抛物线,而是一条直线.利用抛物线定义可推导抛物线的标准方程.应注意抛物线的标准方程有四种不同的形式.【例1】如图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.解答:以直线l1为x轴,线段MN的垂直平分线为y轴,建立直角坐标系,由条件可知,曲线C是以点N为焦点,以l2为准线的抛物线的一段,其中A、B分别为C的端点.设曲线C的方程为y2=2px(p>0)(xA≤x≤xB,y>0),其中xA、xB分别为A、B的横坐标,p=|MN|,所以M(-,0)、N(,0).由|AM|=,|AN|=3,得2pxA=17,①(xA-)2+2pxA=9,②变式1.求与直线l:x=-1相切,且与圆C:(x-2)2+y2=1相外切的动圆圆心P的轨迹方程.解答:设动圆圆心P(x,y),动圆半径为r.由已知条件知因此P点轨迹为以F(2,0)为焦点,l:x=-2为准线的抛物线,又=2.∴动圆圆心P的轨迹方程为y2=8x.求抛物线标准方程常用的方法是待定系数法或轨迹法,标准方程有四种形式,在设方程形式之前,首先要确定抛物线的开口方向.为避免开口不一定而分成y2=2px(p>0)或y2=-2px(p>0)两种情况求解的麻烦,可以设成y2=mx或x2=ny(m≠0,n≠0),若m>0,开口向右,m<0开口向左,m有两解,则抛物线的标准方程有两个【例2】已知如图所示直线l过原点,抛物线C的顶点在原点,焦点在x轴正半轴上,点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.解答:设直线l的方程为y=kx,抛物线C的方程为y2=2px,p>0设(a,b)关于y=kx的对称点坐标为(x0,y0),∴A(-1,0),B(0,8)关于l对称点坐标为(),(),又A、B点在抛物线y2=2px上,则①除以②整理得,k3=(k2-1)3,即k2-k-1=0.变式2.如图,已知抛物线y2=2px(p>0)有一个内接直角三角形,直角顶点在原点,两直角边OA与OB的长分别为1和8,求抛物线方程.解答:设直线OA的方程为y=kx,k≠0,则直线OB的方程为y=-x,由得x=0或x=∴A点坐标为B点坐标为(2pk2,-2pk),由|OA|=1,|OB|=8可得②÷①解方程组得k6=64,即k2=4.则p2=又p>0,则p=,所求抛物线方程为y2=x.可利用定义对曲线定性,由标准方程进行定量分析和研究.【例3】(原创题)如图,已知直线与抛物线y2=2px(p>0)相交于A、B两点,且OA⊥OB,OD⊥AB交AB于D,且点D的坐标为(3,).(1)求p的值;(2)若F为抛物线的焦点,M为抛物线上任一点,求|MD|+|MF|的最小值.解答:(1)设由OA⊥OB,+y1y2=0,即y1y2+4p2=0.-8p+4p2=0,又p>0,则p=2.(2)由抛物线定义知|MD|+|MF|的最小值为D点到抛物线y2=4x准线的距离,又准线方程为x=-...