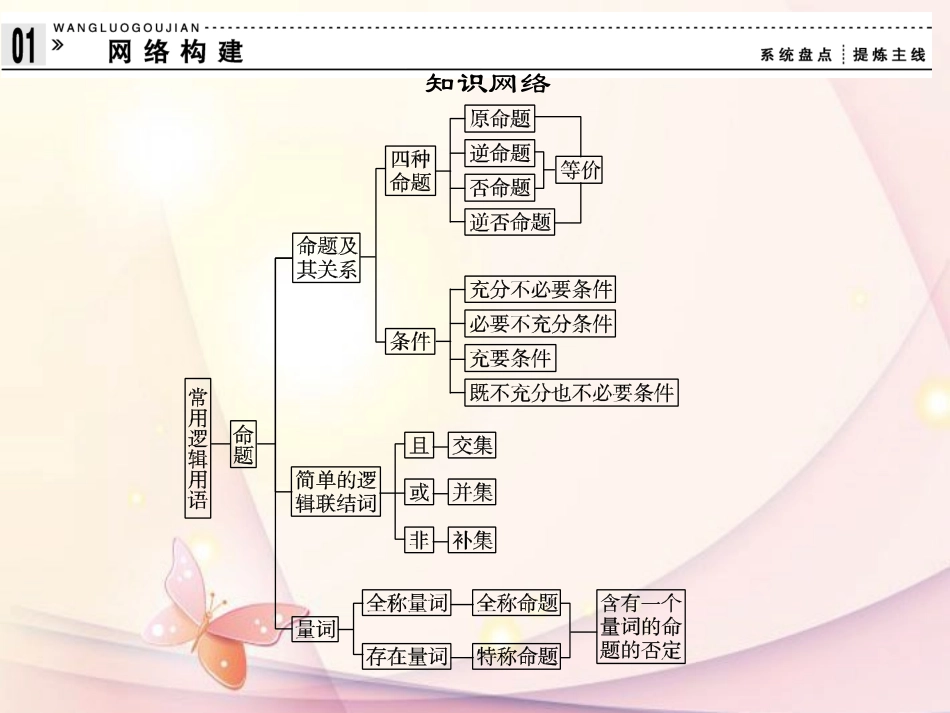
本章归纳整合知识网络要点归纳1.要注意全称命题、特称命题的自然语言之间的转换.2.正确理解“或”的意义,日常用语中的“或”有两类用法:其一是“不可兼”的“或”;其二是“可兼”的“或”,我们这里仅研究“可兼”的“或”.3.有的命题中省略了“且”“或”,要正确区分.4.常用“都是”表示全称肯定,它的存在性否定为“不都是”,两者互为否定;用“都不是”表示全称否定,它的存在性肯定可用“至少有一个是”来表示.(3)p、q“换位”且“换质”:交换原命题的条件和结论,并且同时否定,所得的命题是逆否命题:“若綈q,则綈p”.原命题与它的逆命题、原命题与它的否命题之间的真假是不确定的,而原命题与它的逆否命题(它的逆命题与它的否命题)之间在真假上是始终保持一致的:同真同假.【例1】判断下列命题的真假.(1)若x∈A∪B,则x∈B的逆命题与逆否命题;(2)若00;②∃x0∈Q,13x20+12x0+1不是有理数;③∃α0,β0∈R,使sin(α0+β0)=sinα0+sinβ0;④∃x0,y0∈Z,使3x0-2y0=10.A.1B.2C.3D.4解析①中x2+x+3=(x+12)2+114≥114>0,故①是真命题.②中x∈Q,13x2+12x+1一定是有理数,故②是假命题.③中α=π4,β=-π4时,sin(α+β)=0,sinα+sinβ=0,故③是真命题.④中x0=4,y0=1时,3x0-2y0=10成立,故④是真命题.答案C专题五全称命题、特称命题的否定1.写命题的否定时,关键是确定命题的类型.2.判断命题的否定的真假时,可直接判断该命题,也可判断原命题的真假,利用原命题和命题的否定的真假性相反下结论.(2)命题p:∃m0∈R,使方程x2+m0x+1=0有实数根,则“綈p”形式的命题是().A.∃m0∈R,使得方程x2+m0x+1=0无实根B.对∀m∈R,方程x2+mx+1=0无实根C.对∀m∈R,方程x2+mx+1=0有实根D.至多有一个实数m,使得方程x2+mx+1=0有实根答案(1)C(2)B【例6】写出下列命题的否定,并判断真假:(1)不论m取什么实数,方程x2+x-m=0必有实数根.(2)存在一个实数x0,使得x20+x0+1≤0.(3)等圆的面积相等,周长相等.(4)对任意角α,都有sin2α+cos2α=1.解(1)∃m0∈R,方程x2+x-m0=0无实根,真命题.(2)∀x∈R,x2+x+1>0,真命题.(3)有的等圆的面积不相等或周长不相等,假命题.(4)∃α0使得sin2α0+cos2α0≠1,假命题.【例7】已知命题p:任意非零向量a、b、c,若a·(b-c)=0,则b=c.写出其否定和否命题,并说明真假.解綈p:存在非零向量a、b、c,若a·(b-c)=0,则b≠c.綈p为真命题.否命题:任意非零向量a、b、c,若a·(b-c)≠0,则b≠c.否命题为真命题.命题趋势命题真假的判断,充要条件的判定,含一个量词的命题的否定是高考考查的重点.其中命题真假的判断和充要条件的判定往往与其他知识相结合,考查相关知识点,体现了在知识交汇点处命题的特点,一般以选择题的形式出现,难度不大.常见的考查角度有以下几种:2.充分条件、必要条件和充要条件是对命题进行研究和考查的重要途径,是高考重点考查的内容,往往在不同知识点的交汇处进行命题,考查面十分广泛,涵盖函数、立体几何、不等式、向量、三角等内容.通过对命题条件和结论的分析,考查对数学概念的准确记忆和深层次的理解.3.逻...