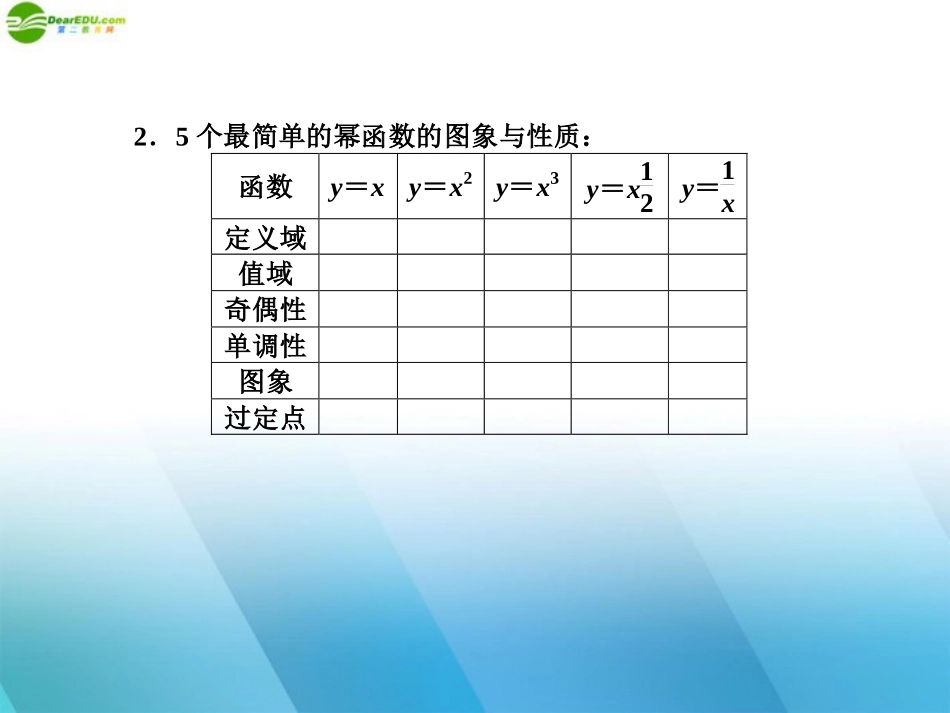
第九节幂函数第九节幂函数教材面面观1.一般地,函数________叫做幂函数,其中x是自变量,α是常数.注意幂函数中底数是自变量,幂指数是常数,这与指数函数是不同的,指数函数中底数是常数,幂指数是自变量.答案y=xα2.5个最简单的幂函数的图象与性质:函数y=xy=x2y=x3y=x12y=1x定义域值域奇偶性单调性图象过定点答案函数y=xy=x2y=x3y=x12y=1x定义域RRR{x|x≥0}{x|x≠0}值域R{y|y≥0}R{y|y≥0}{y|y≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在R上递增在(-∞,0)上递减,在(0,+∞)上递增在R上递增在(0,+∞)在(-∞,0)和(0,+∞)上递减图象过定点(1,1)考点串串讲1.幂函数的图象幂函数y=xα,当α=13,12,1,2,3时的图象见图(1)所示;当α=-2,-1,-12时的图象见图(2)所示;2.幂函数的性质(1)α>0时;①图象都通过点(0,0),(1,1);②在第一象限内,函数值随x的增大而增大,即在(0,+∞)上是增函数.(2)α<0时;①图象都通过点(1,1);②在第一象限内,函数值随x的增大而减小,即在(0,+∞)上是减函数.③在第一象限内,图象向上与y轴无限地接近,向右与x轴无限地接近.3.比较大小利用幂函数和指数函数的单调性可以比较幂值的大小,具体方法如下:(1)当幂的底数相同,指数不同时,可以利用指数函数的单调性比较;(2)当幂的底数不同,指数相同时,可以利用幂函数的单调性比较;(3)当幂的底数和指数都不相同时,一种方法是作商,通过商与1的大小关系确定两个幂值的大小;另一种方法是运用媒介法,即找到一个中间值,通过比较两个幂值与中间值的大小,从而确定两个幂值的大小;(4)比较多个幂值的大小一般采用媒介法,即先判断这组数中每个幂值与0,1等数的大小关系,据此将它们分成若干组,然后将同一组内的各数再利用相关方法进行比较,最终确定各数之间的大小关系.典例对对碰题型一幂函数定义例1若幂函数y=(m2+3m-17)24xmm-的图象不过原点,求实数m的取值范围.解析依题意,得m2+3m-17=14m-m2<0⇒m=-6或m=3,m<0或m>4.所以m=-6.点评问题切入点幂函数的形式是y=x2.因此m2+3m-17=1,另一方面图象不过原点,必有4m-m2<0,从而求出m.熟练掌握并理解幂函数定义及性质是解题的关键.变式迁移1函数f(x)=(m2-m-1)xmm223--是幂函数,且在x∈(0,+∞)上是减函数,则实数m的值为()A.2B.3C.4D.5答案A解析由题知m2-m-1=1,得m=-1或m=2,再验证m2-2m-3<0,得m=2.故选A.题型二定义域问题例2求下列函数的定义域:(1)y=x35;(2)y=x14;(3)y=x23-;(4)y=x34-.解析把分数指数幂化为根式(1)y=x35=5x3,其定义域为R;(2)y=x14=4x,其定义域为[0,+∞);(3)y=x23-=13x2,其定义域为(-∞,0)∪(0,+∞);(4)y=x34-=14x3,其定义域为(0,+∞).点评注意:①分母不能为0;②偶次根号下必须为非负实数;③零的零次方没有意义;④奇次根号下不作限制.变式迁移2设α∈{-1,1,12,3},则使函数y=xα的定义域为R且为奇函数的所有α的值为________.答案1,3解析定义域为R说明幂指数是正数且幂指数不等于12,是奇函数说明α=1,3.题型三幂函数的图象例3已知点(2,2)在幂函数f(x)的图象上,点(-2,14)在幂函数g(x)的图象上,问当x为何值时,有(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)<g(x).分析首先要理解幂函数是形式定义,y=xα,然后根据函数图象可以解决.解析设f(x)=xα,因为点(2,2)在幂函数f(x)的图象上,将点(2,2)代入f(x)=xα中,得2=(2)a,解得a=2,∴f(x)=x2;设g(x)=xb, 点(-2,14)在幂函数g(x)的图象上,将点(-2,14)代入g(x)=xb中,得14=(-2)b,解得b=-2,∴g(x)=x-2.在同一坐标系下作出f(x)=x2与g(x)=x-2的图象如图所示.由图象可知:(1)当x>1,或x<-1时,f(x)>g(x);(2)当x=1,或x=-1时,f(x)=g(x);(3)当-1<x<1,且x≠0时,f(x)<g(x).点评(1)幂函数的一般形式是y=xα(α为常数),要求幂函数只要解出α即可;(2)函数的图象在解方程和不等式时有着重要的作用;(3)本题注意g(x)=x-2的定义域是{x|x≠0},即求幂函数的解析式问题的关键是...