高中数学 322对数函数(1)课件 苏教版必修1 课件VIP免费

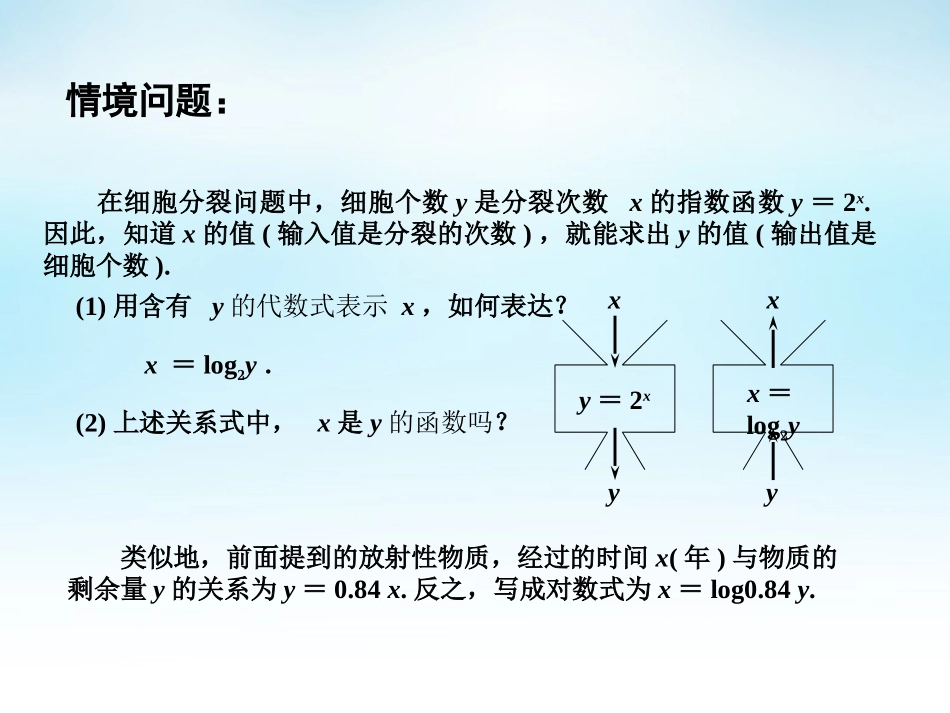
高中数学必修高中数学必修１１高中数学必修高中数学必修１１情境问题：在细胞分裂问题中，细胞个数y是分裂次数x的指数函数y＝2x.因此，知道x的值(输入值是分裂的次数)，就能求出y的值(输出值是细胞个数).(1)用含有y的代数式表示x，如何表达？x＝log2y．(2)上述关系式中，x是y的函数吗？xy＝2xyxyx＝log2y类似地，前面提到的放射性物质，经过的时间x(年)与物质的剩余量y的关系为y＝0.84x.反之，写成对数式为x＝log0.84y.数学建构：2．对数函数的定义域是什么？3．对数函数的值域是什么？一般地，函数y＝logax(a＞0且a≠1)叫做对数函数．对数函数的定义：1．在对数函数的解析式y＝logax中，为什么要规定a＞0且a≠1？思考问题：数学应用：例1．在同一个直角坐标系中分别画出下列函数的图象．(1)y＝log2x与y＝2x；xyOy＝2xy＝log2x121(2)log2xyxy与xyO12xy12logyx数学建构：一般地，对数函数y＝logax在底数a＞1及0＜a＜1这两种情况下的图象和性质如下表所示：a＞10＜a＜1图象定义域值域性质R(0，＋)R上的减函数图象恒过定点(1，0)，即x＝1时，y＝0对数函数的图象与性质：R上的增函数xyO1xyO1数学建构：xyOy＝x12logyx函数y＝ax与y＝logax(a＞0且a≠1)是互为反函数：一般地，如果函数y＝f(x)存在反函数，那么它的反函数记为y＝f－1(x)，且函数y＝f－1(x)的图象与y＝f(x)的图象关于直线y＝x对称．xyOy＝2xy＝log2xy＝x12xy数学应用：例2．求下列函数定义域：(1)y＝log0.2(4－x)y＝log(5－x)(2x－3)y＝log0.5x2(2)y＝loga(a＞0且a≠1)1x变式：数学应用：小结：在解决比较两个数的大小问题时，一般情况下是将其看作一个函数的两个函数值，利用函数的单调性直接比较它们的大小，如(1)、(2)．当两个数不能直接比较时，我们可以将其与一个已知的过渡数进行比较大小，从而得出该两数的大小关系．常用来过渡的值有0或±1等，根据实际问题也可能是其它数值，此外还要心中有函数的图象．例3．比较大小：(1)log23.4，log23.8；(2)log0.51.8，log0.52.1；(3)log75，log67；(4)log3，log0.31.5；(5)log25，log748；(6)log3.42；log1.12．利用单调性利用中间量“1”利用中间量“0”利用图象性质利用中间量“2”数学应用：求函数y＝log0．5(1－x)＋log0．5(x＋3)的最小值．解下列方程：(1)log2(3x)=log2(2x＋1)(2)log5(2x＋1)=log5(x2－2)(3)=lg(x－1)lgx－1小结：对数函数的定义：函数y＝logax(a＞0，a≠1)叫做对数函数．对数函数的定义域为(0，＋)，值域为R．对数函数的图象和性质：对数函数的图象恒过点(1，0)，当0＜a＜1时，对数函数在(0，＋)上递减；当a＞1时，对数函数在(0，＋)上递增．作业：课本P87习题2，3，4.