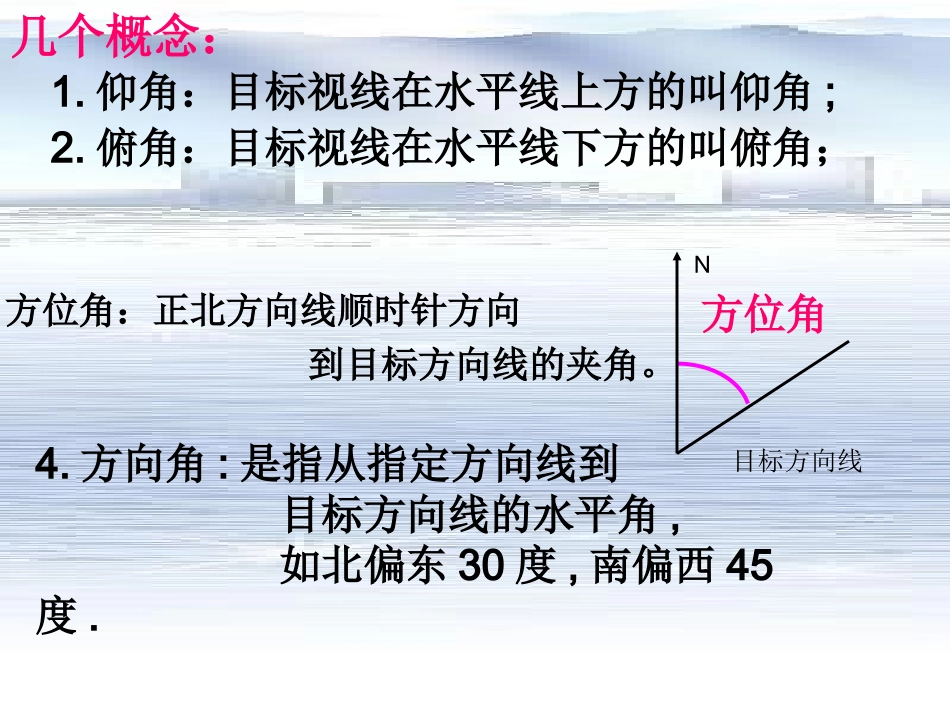
正弦、余弦定理的应用举例(3)解应用题的一般步骤1.审题(分析)理解题意,明确背景,熟悉已知条件,了解所需要的条件(或量),明确试题的所求内容;画出示意图.2.建立数学模型(写出已知求解)把实际问题转化为数学问题.3.解答数学模型解答数学问题.4.总结(检验)与问题所求量进行联系,总结作答1.仰角:目标视线在水平线上方的叫仰角;2.俯角:目标视线在水平线下方的叫俯角;方位角N目标方向线4.方向角:是指从指定方向线到目标方向线的水平角,如北偏东30度,南偏西45度.几个概念:3.方位角:正北方向线顺时针方向到目标方向线的夹角。0001.,,7567.5,,3254.0.,,(0.1,0.01).AnmileBBnmileCACnmile问题如图一艘海轮从出发沿北偏东的方向航行后到达海岛然后从出发沿北偏东的方向航行后到达海岛如果下次航行直接从出发到达此船应该沿怎样的方向航行需要航行多少距离角度精确到距离精确到问题1:一艘海轮从A出发,沿北偏东75°的方向航行67.5nmile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0nmile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01nmile)?解:在△ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,15.113137cos0.545.6720.545.67cos22222ABCBCABBCABAC,3255.015.113137sin0.54sinsinsinsinACABCBCCABABCACCABBC根据正弦定理,所以,∠CAB=19.0°,75°-∠CAB=56.0°.答:此船应该沿北偏东56.0°的方向航行,需要航行113.15nmile.练习:课本16页222222222sinsin1sin22(coscoscos).ABCabABcCabcbcAcaBabC问题2:在中,求证:();()练习:课本18页作业课本20页9.10.14学案第四课练习