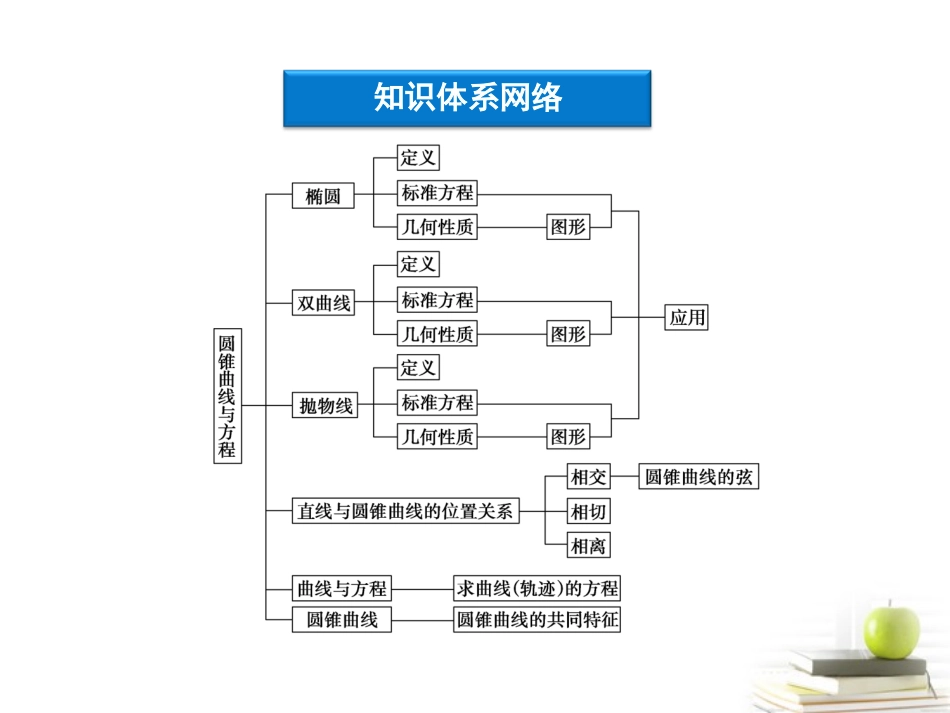
本章优化总结专题探究精讲本章优化总结知识体系网络章末综合检测知识体系网络专题探究精讲圆锥曲线的定义(1)平面内满足|PF1|+|PF2|=2a(2a>|F1F2|)的点P的轨迹叫作椭圆,定义可实现椭圆上的点到两焦点的距离的相互转化.(2)平面内满足||PF1|-|PF2||=2a(2a<|F1F2|)的点P的轨迹叫作双曲线,|PF1|-|PF2|=2a(2a<|F1F2|)表示焦点F2对应的一支,定义可实现双曲线上的点到两焦点的距离的相互转化.(3)平面内与一个定点F和一条定直线l(不经过点F)距离相等的点的轨迹叫作抛物线,定义可实现抛物线上的点到焦点与到准线距离的相互转化.例例11(2010年高考辽宁卷)设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为-3,那么|PF|=()A.43B.8C.83D.16【解析】如图所示,直线AF的方程为y=-3(x-2),与准线方程x=-2联立得A(-2,43).设P(x0,43),代入抛物线方程y2=8x,得8x0=48,∴x0=6,∴|PF|=x0+2=8,选B.【答案】B圆锥曲线的性质(1)圆锥曲线的范围往往作为解题的隐含条件.(2)椭圆、双曲线有两条对称轴和一个对称中心,抛物线只有一条对称轴.(3)椭圆有四个顶点,双曲线有两个顶点,抛物线只有一个顶点.(4)双曲线焦点位置不同,渐近线方程不同.(5)圆锥曲线中基本量a,b,c,e,p的几何意义及相互转化.例例22椭圆x2a2+y2b2=1(a>b>0)的焦距为2c,若直线y=2x与椭圆的一个交点的横坐标恰为c,则椭圆的离心率等于()A.2-22B.22-12C.3-1D.2-1【解析】当x=c时,由c2a2+y2b2=1,得y=±b2a,所以2c=b2a=a2-c2a=a-c2a.因此,2ca=1-c2a2⇒e2+2e-1=0,解得e=-1±2.因为00,即m2<3k2+1,①∴xP=xM+xN2=-3mk3k2+1,从而yP=kxP+m=m3k2+1,∴kAP=yP+1xP=-m+3k2+13mk,又|AM|=|AN|,∴AP⊥MN,则-m+3k2+13mk=-1k,即2m=3k2+1,②把②代入①得2m>m2,解得00,解得m>12,故所求m的取值范围是(12,2).圆锥曲线中的定点、定值问题往往与圆锥曲线中的“常数”有关,如椭圆的长、短轴,双曲线的虚、实轴;抛物线的焦点等.可以通过直接计算而得到,另外还可以用“特例法”和“相关曲线系法”求得.圆锥曲线中的最值问题,通常有两类:一类是有关长度、面积等的最值问题;一类是圆锥曲线中有关几何元素的最值问题.这两类问题的解决往往要通过回归定义,结合几何知识,建立圆锥曲线中的定点、定值、最值问题目标函数,利用函数的性质或不等式知识,三角函数有界性,以及数形结合、设参、转化代换等途径来解决.特别注意函数思想,观察分析图形特征,利用数形结合等思想方法.例例44如图所示,过抛物线y2=2px的顶点O作两条互相垂直的弦交抛物线于A、B两点.求:△AOB面积的最小值.【解】设直线AB的方程为y=k(x-a),A(x1,y1),B(x2,y2).联立方程y2=2px,y=kx-a,消去x得ky2-2py-2pak=0,则y1y2=-2pa.又OA⊥OB.∴y1y2=-x1x2.由方程组消去y,得k2x2-(2k2a+2p)x+k2a2=0,则x1·x2=a2.因此,a2=2pa.∴a=2p.故直线AB过定点M(2p,0).∴S△AOB=S△AOM+SBOM=12|OM|(|y1|+|y2|)≥p(2|y1y2|).又y21=2px1,y22=2px2,∴(y1y2)2=4p2x1x2.又 y1y2=-x1x2,于是|y1y2|=4p2.故S△AOB的最小值为4p2.求曲线方程是解析几何的基本问题之一,其求解的基本方法有:(1)直接法:当动点与已知条件发生...