高中数学 423函数建模案例课件 北师大版必修1 课件VIP免费

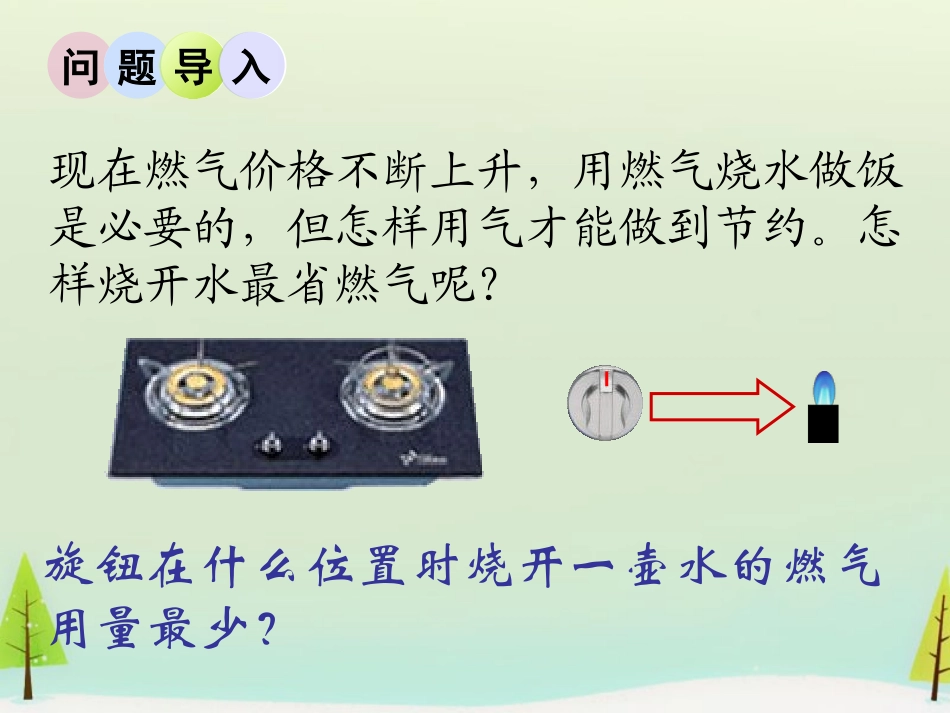
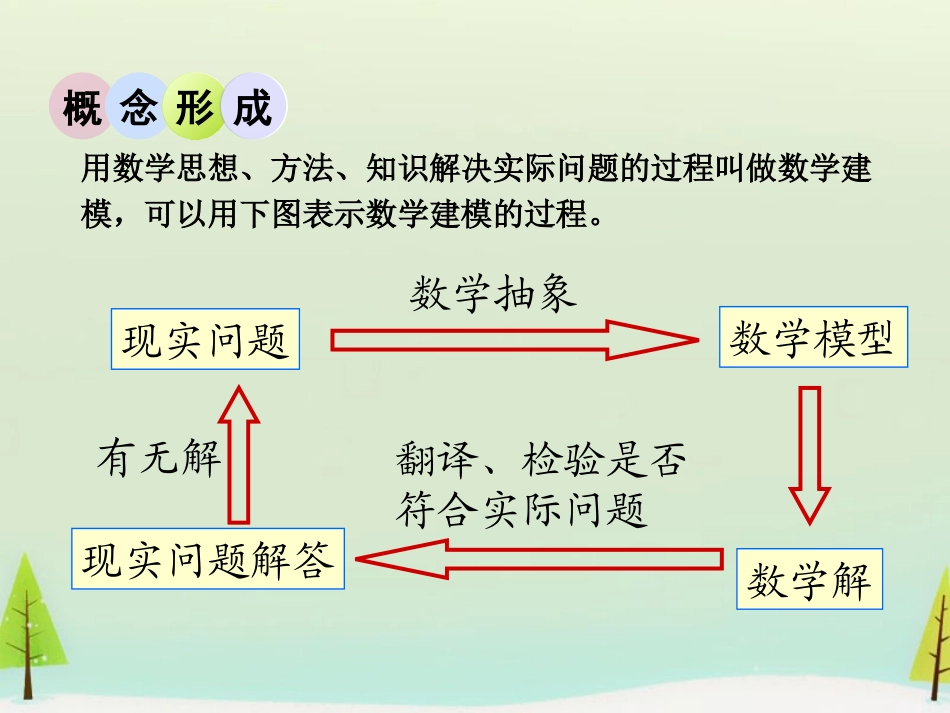
§2.3函数建模案例现在燃气价格不断上升，用燃气烧水做饭是必要的，但怎样用气才能做到节约。怎样烧开水最省燃气呢？旋钮在什么位置时烧开一壶水的燃气用量最少？问题导入现实问题数学模型数学抽象数学解有无解现实问题解答翻译、检验是否符合实际问题概念形成用数学思想、方法、知识解决实际问题的过程叫做数学建模，可以用下图表示数学建模的过程。一、建立数学模型解决问题的方案0°18°36°54°72°90°例题分析1.准备燃气灶和一只水壶,选定旋钮五个位置:18°,36°,54°,72°,90°2.在一个位置上分别记录烧开一壶水所需的时间和所用燃气量.3.利用数据拟合函数,建立旋钮位置与烧开一壶水燃气用量的函数解析式.4.利用函数解析式求最小用气量.5.对结果的合理性作出检验分析.一、建立数学模型解决问题的方案项目位置燃气表开始时读数/m3燃气表水开时读数/m3所用燃气量/m318°9.0809.2100.13036°8.9589.0800.12254°8.8198.9580.13972°8.6708.8190.14990°8.4988.6700.172二、实验记录相关数据0.1720.1490.1390.1220.1300.10.218°36°54°72°90°燃气用量/m3旋钮角度二、实验在直角坐标系上标出旋钮位置与烧开一壶水燃气用量的点三、拟合函数根据燃气用量的变化过程,用二次函数近似表示设函数式为y=ax2+bx+c取三点(18,0.130),(36,0.122),(90,0.172)代入函数式,得方程组172.09090122.03636130.01818222cbacbacba解得a=1.903×10-5,b=-1.4722×10-3,c=1.5033×10-1则函数式为y=1.903×10-5x2-1.4722×10-3x+1.5033×10-1四、求最小用气量求燃气用量最少时的旋钮位置,实际上是求函数的最小值点x0abx20abacy442039109033.12104722.15352315109033.14104722.1105033.1109033.1431218.0m五、检验分析取旋转39°的旋钮位置，烧一壶开水，所得实际用气量是不是0.1218m3?如果基本吻合,就可以依此作结论.如果相差大,特别是用量大于0.122,最小值点就不是39°,说明三个数据取得不好,可以换另外的点重新计算,然后再检验,直至结果与实际比较接近就可以了.项目位置开始时刻水开时刻燃气表开始时读数/m3燃气表水开时读数/m318°6:066:259.0809.21036°5:496:058.9589.08054°5:355:498.8198.95872°5:225:348.6708.81990°5:095:198.4988.670下面是燃气灶旋钮在不同位置时烧开一壶水所需的时间及燃气用量表(1)分析旋钮在不同位置时烧水用时间的规律,确定最省时的旋钮位置05101520050100旋钮位置用时/分钟减函数,最省时的旋钮位置是90°(2)用燃气烧水,能否做到最省时又最省气?00.050.10.150.2050100旋钮位置用气量不能做到最省时又最省气某地新建一个服装厂，从今年7月份开始投产，并且前4个月的产量分别为1万件、1.2万件、1.3万件、1.37万件.由于产品质量好，服装款式新颖，因此前几个月的产品销售情况良好.为了在推销产品时，接收定单不至于过多或过少，需要估测以后几个月的产量，你能解决这一问题吗？随堂练习•探索过程如下：(1）首先建立直角坐标系，画出散点图；(2）根据散点图设想比较接近的可能的函数模型：•一次函数模型：•二次函数模型：•幂函数模型：•指数函数模型：()(0);fxkxbk2()(0);gxaxbxca12()(0);hxaxba()xlxabc)1,0,0(bba实际情境提出问题数学模型数学结果检验可用结果不合乎实际合乎实际数学建模的过程小结反思