高中数学二次不等式不等式二次方程课件新人教版必修5 课件VIP免费

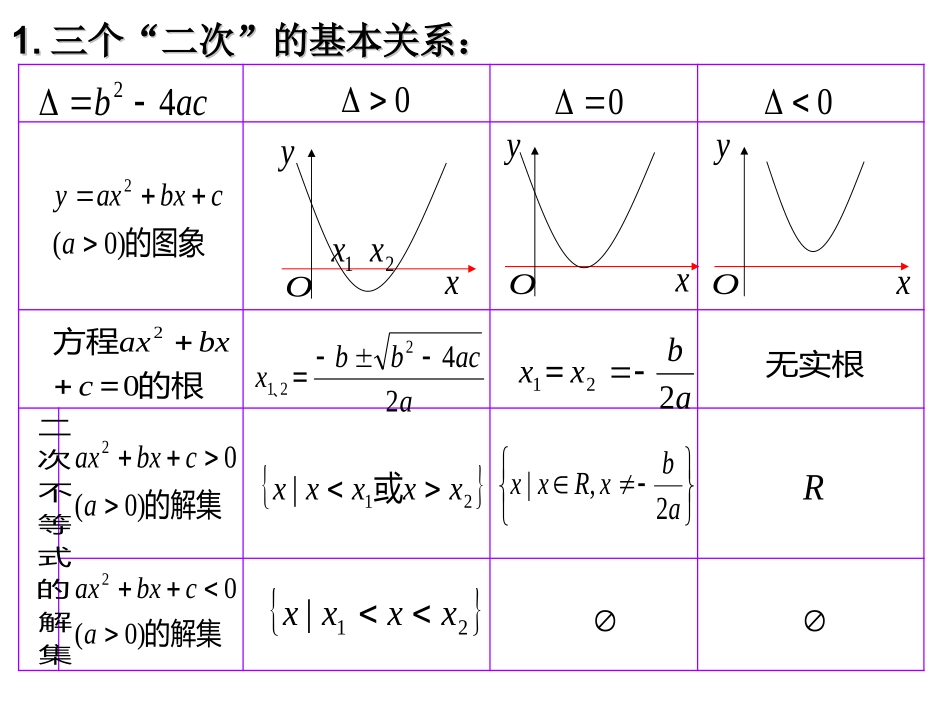
形如形如axax22+bx+c>0+bx+c>0的不等式的的不等式的解题策略解题策略Oxy的基本关系，能借助这三个“二的基本关系，能借助这三个“二次”次”容容内内分分析析含参数一元二次不等式是含参数一元二次不等式是一类一类重要的不等式，也是高中数学的一重要的不等式，也是高中数学的一个重要的工具，通过本节的学习，个重要的工具，通过本节的学习，同学们要深刻地理解同学们要深刻地理解的基本关系，运用数形结合的思想的基本关系，运用数形结合的思想方法去分析、解决相关问题。方法去分析、解决相关问题。三个“二次”1.1.三个“二次”的基本关系：三个“二次”的基本关系：acb42000的图象)0(2acbxaxy的根＝方程02cbxax的解集)0(02acbxax的解集)0(02acbxaxxyOxyOxyO1x2xaacbbx24221＝、abxx221＝无实根21|xxxxx或21|xxxxabxRxx2,|R集解的式等不次二例1.x2+5ax+6>0解：由题意，得：⊿=25a2－241.当⊿=25a2－24>0，;22224525224525aaxaaxx或2.当⊿=25a2－24=0，3.当⊿=25a2－24<0,解集为：解集为：;25axRxx且时652652即a解集为：R.时或即652652aa时即652a二、典型题选讲(一)含参不等式的解法变题1.x2+5ax+6a2>0解：因式分解，得:（x+3a)(x+2a)>0，方程（x+3a)(x+2a)＝0的两根为－3a、－2a.①当－3a>－2a即a<0时，解集为：{x︱x>－3a或x<－2a};②当－3a=－2a即a=0时，解集为：{x︱x∈R且x≠0}；③当－3a<－2a即a>0时，综上：当a>0时，解集为：{x︱x>－2a或x<－3a}.当a=0时，解集为：{x︱x∈R且x≠0};当a<0时，解集为：{x︱x>－3a或x<－2a};解集为：{x︱x>－2a或x<－3a}.原不等式为x2>0变题2.ax2+(6a+1)x+6>0二、当a≠0时，6|解集为xx①当a<0时，,01aaxx16解集为一、当a=0时，②当a>0时，01a⑴时即当616,1aa6或1:解集为xaxx⑶⑵时即当616,1aa6或:解集为xRxx时即当6106,1aaaxxx1或6:解集为6,1两根为061方程axax的∴综上，得;1x6x0.1aa时，解集为当;10.2xxa解集为时当，;1或6解集为时610当.3axxxa，;661.4xRxxa且解集为时当，.6161.5xaxxa或时，解集为当06x1x因式分解，得：a评注评注解形如解形如axax22+bx+c+bx+c>>00的不等式时分类讨的不等式时分类讨论的标准有：论的标准有：11、讨论、讨论aa与与00的大小；的大小；22、讨论、讨论⊿⊿与与00的大小；的大小；33、讨论两根的大小；、讨论两根的大小；例2关于x的二次不等式a2x2+6ax+9－b2≤0的解集是[－1，2]，求a,b解：依题意知方程a2x2+6ax+9—b2=0的两根为—1,2∴变题：已知|ax+3|≤b（且b＞0）的解集为{x|－1≤x≤2}，求实数a，b的值。9696baba或解得：解：|ax+3|≤b(b>0)两边平方，得(ax+3)2≤b2∵b>0,舍去后一组解∴a=－6,b=99696baba或解得：即：a2x2+6ax+9-b2≤0∴a2x2+6ax+9—b2=0的两根为—1,2219216222abaa（1）二次不等式ax2+bx+c>0恒成立例题：已知关于x的不等式：(a-2)x2+(a-2)x+1≥0恒成立，解：由题意知：①当a-2=0，即a=2时，不等式化为②当a-2≠0，即a≠2时，原题等价于220(2)4(2)0aaa综上：试求a的取值范围.1≥0，它恒成立，满足条件.2(2)(6)0aaa即226aa即26a所以26a知识概要（2）二次不等式ax2+bx+c<0恒成立2040abac2040abac（3）二次不等式ax2+bx+c≥0恒成立2040abac（4）二次不等式ax2+bx+c≤0恒成立0402acba(二)含参不等式恒成立的问题三、课堂小结1、解含参数的不等式2、已知不等式的解集，求参数的值或范围不等式中的恒成立问题一、内容分析二、运用的数学思想1、分类讨论的思想3、等与不等的化归思想2、数形结合的思想用图象分离参数后用最值函数、、、321四、课后作业：1.解下列不等式：①022kkxx②2(3)2(1)0xaxa2.关于x的不等式：2(1)(1)10kxkx恒成立，求k的范围.