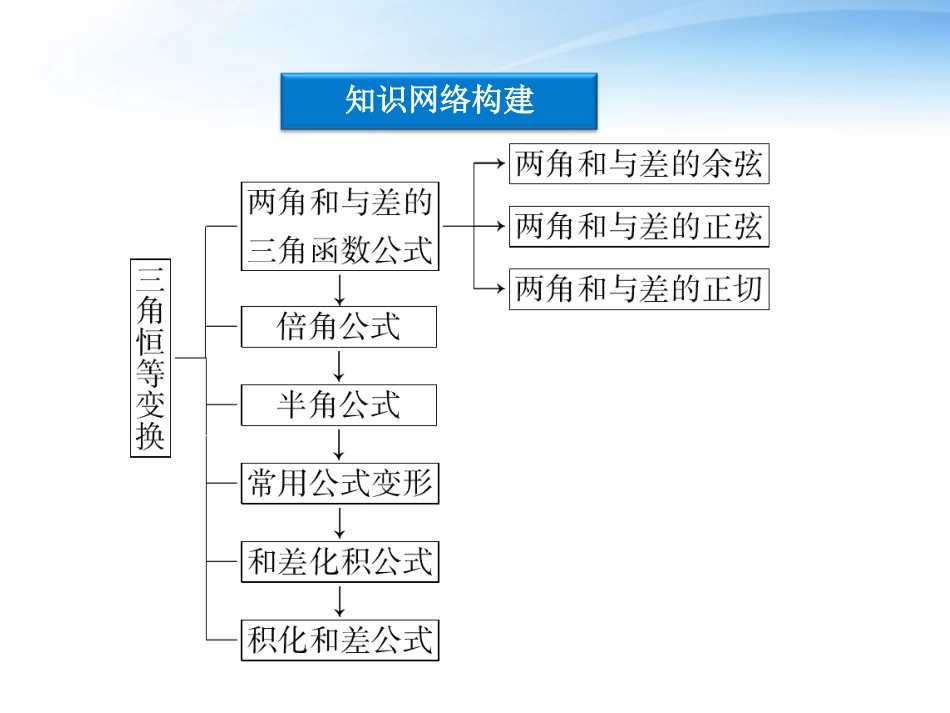
本章优化总结本章优化总结知识网络构建专题探究精讲章末综合检测知识网络构建专题探究精讲三角函数式的化简求值问题三角函数求值主要有三种类型,即:(1)“给角求值”,一般给出的角都是非特殊角,从表面看较难,但仔细观察就会发现这类问题中的角与特殊角都有一定的关系,如和或差为特殊角,当然还有可能需要运用诱导公式.(2)“给值求值”,即给出某些角的三角函数式的值,求另外一些三角函数的值,这类求值问题关键在于结合条件和结论中的角,合理拆、配角.当然在这个过程中要注意角的范围.(3)“给值求角”,本质上还是“给值求值”,只不过往往求出的是特殊角的值,在求出角之前还需结合函数的单调性确定角,必要时还要讨论角的范围.例例11已知sin(α+β)=7210,sin(α-β)=-22,求tanαtanβ的值.【分析】把已知两式展开,联立解“方程组”求出“sinαcosβ和cosαsinβ”,再求sinαcosβcosαsinβ即可.【解】由sin(α+β)=7210,得sinαcosβ+cosαsinβ=7210;①由sin(α-β)=-22,得sinαcosβ-cosαsinβ=-22.②①+②得:sinαcosβ=210;①-②得:cosαsinβ=6210.sinαcosβcosαsinβ=tanαtanβ=2106210=16.【点评】给出某些角的三角函数值,求另外一些角的三角函数值,解题的关键在于“变角”.使其角相同或具有某种关系,解题的基本方法是:①将待求式用已知三角函数表示.②将已知条件进行转化推出可用的结论.其中“凑角法”是解决此类问题的常用技巧.解题时首先是分析已知式与待求式之间角、函数、结构间的差异,有目的地将已知式、待求式的一方或两方加以变换,找出它们之间的联系,最后求出待求式的值.已知0<α<π4,0<β<π4,且3sinβ=sin(2α+β),4tanα2=1-tan2α2,求α+β的值.例例22【分析】本题主要考查三角函数式的恒等变形及已知三角函数值求角,因为2α+β=α+(α+β),β=(α+β)-α,可先将条件式3sinβ=sin(2α+β)展开后求α+β的正切值.【解】 3sinβ=sin(2α+β),即3sin(α+β-α)=sin(α+β+α),整理得2sin(α+β)cosα=4cos(α+β)sinα.即tan(α+β)=2tanα.又 4tanα2=1-tan2α2,∴tanα=2tanα21-tan2α2=12,tan(α+β)=2tanα=2×12=1. α+β∈(0,π2),∴α+β=π4.【点评】(1)给值求角实质上也转化为“给值求值”,关键也是变角.把所求的角用含已知其值的角的式子表示,即先求出该角的某一个三角函数值,由所求的函数值结合该函数的单调区间求得角,但不要忽视对所求角范围的讨论.(2)对于通过变形转化为已知三角函数值求角的问题,关键是对角的范围进行讨论.注意合理利用不等式的性质,必要时,根据三角函数值,缩小角的范围,从而求出准确角.另外,求角一般都通过三角函数值来实现,但求角的哪一种函数值,往往有一定的规律.若α∈(0,π),则求cosα;若α∈(-π2,π2),则求sinα等.化简sin50°(1+3tan10°).例例33【分析】按照一般的解题思路是将切函数化为弦函数,然后通分,利用相关的倍角公式进行化简;如果观察题中的角度:50°和10°最好能凑出特殊角60°,而括号内的式子:1+3tan10°,可将3写成tan60°,则凑出了两角差正切公式的形式,进而可约分化简.【解】法一:原式=sin50°1+3sin10°cos10°=sin50°·cos10°+3sin10°cos10°=sin50°·212cos10°+32sin10°cos10°=sin50°·2sin40°cos10°=cos40°·2sin40°cos10°=sin80°cos10°=1.法二:原式=sin50°(1+tan60°tan10°)=sin50°·tan60°-tan10°tan50°=cos50°(tan60°-tan10°)=cos50°sin60°cos10°-cos60°sin10°cos60°cos10°=cos50°sin50°cos60°cos10°=sin50°cos50°12cos10°=sin100°cos10°=1.【点评】给角求值的解题规律是恰当地运用诱导公式,合理地进行角的变换,运用和角公式、二倍角公式、积化和差与和差化积公式、万能代换公式和半角公式,使其转化为特殊角的三角函数值的求解问题.给角求值中要注意当角较大时,应先利用诱导公式,这样能使角之间的关系更明确,这也是给角求值...