高中数学：223(双曲线的几何性质2)江苏专用课件(苏教版选修1-1) 课件VIP免费

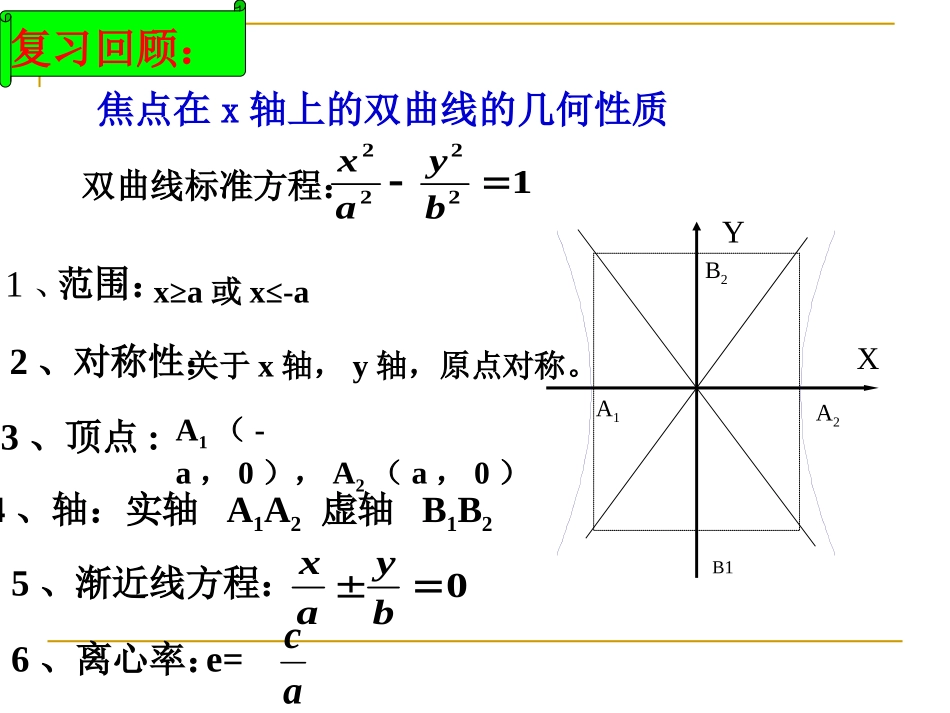
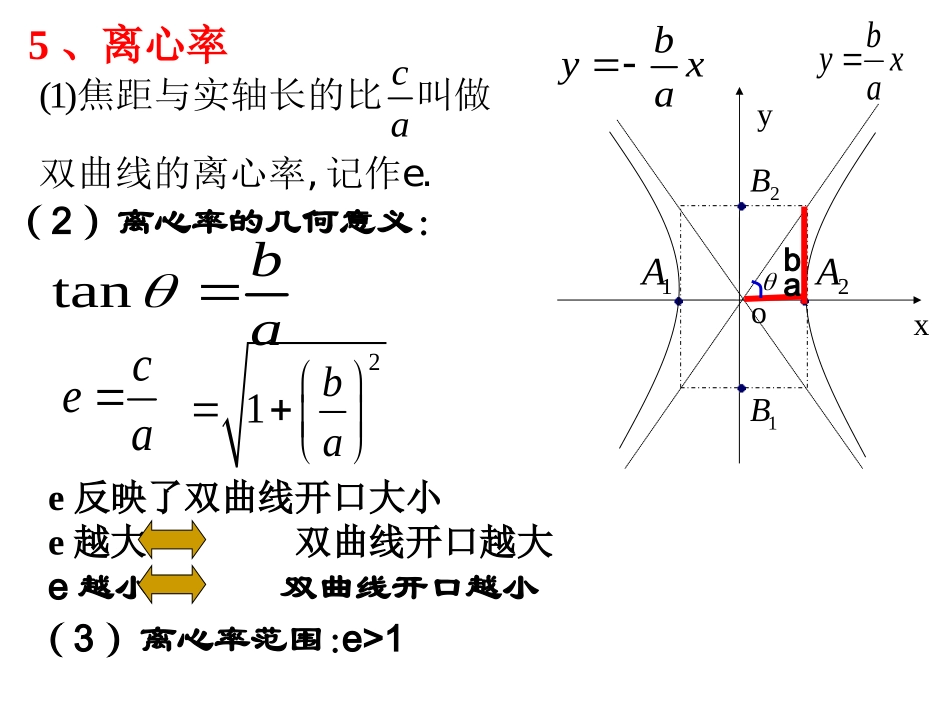
焦点在x轴上的双曲线的几何性质双曲线标准方程：YX12222byax0byax1、范围：x≥a或x≤-a2、对称性：关于x轴，y轴，原点对称。3、顶点:A1（-a，0），A2（a，0）4、轴：实轴A1A2虚轴B1B2A1A2B1B25、渐近线方程：6、离心率：e=ac复习回顾：5、离心率e反映了双曲线开口大小e越大双曲线开口越大e越小双曲线开口越小cea1A2A1B2Bxyobyxabyxa(1)ca焦距与实轴长的比叫做双曲线的离心率,记作e.（3）离心率范围：（2）离心率的几何意义：e>1abtanba21baxyo22221(0,0)yxabab双曲线的几何性质-aab-b（1）范围:,,yayaxR（2）对称性:关于x轴、y轴、原点都对称（3）顶点:(0,-a)、(0,a)（4）渐近线:ayxb（5）离心率:ace例1.求下列双曲线的渐近线方程，并画出图像：149).122yx解：1),92a42b,3a2b2)把方程化为标准方程19422xy,42a92b,2a3bx32y＝渐近线方程是x.32y＝渐近线方程是149).222yx0xy如何记忆双曲线的渐进线方程？例2:求双曲线的实半轴长、虚轴长、焦点坐标、顶点坐标、离心率、渐近线方程。解:由题意可得实半轴长:虚轴长:焦点坐标:离心率:渐近线方程:32yxa=222143xy223b(7,0),(7,0)72cea顶点坐标:(-2,0)，(2,0)21?3y2x问:若双曲线的方程为呢43a24b(0,7),(0,7)213cea32yx(0,3),(0,3)请你写出一个以为渐近线的双曲线方程.32yx你能写出所有以为渐近线的双曲线方程吗?32yx22(0)43xy例3．已知双曲线的焦点在y轴上，焦距为16，离心率是4/3，求双曲线的标准方程。,162c解：由题意得.8c34ac又则解得,6a.286822222acb轴上双曲线的焦点在又y.1283622xy为所求双曲线的标准方程已知双曲线的中心在原点,oxy解：4,2)x21y4xM（的交于＝与渐近线＝点作直线过Q32,xx21y轴上在的下方，即双曲线焦点＝点在直线M1ba2222yx设双曲线方程为得到入上式代），把双曲线经过点（,)3,4(34,1,4)2),122ba解得由例4．已知双曲线的渐近线是，并且双曲线过点02yx)3,4(M求双曲线方程。Q4M1b)3(a422221)x21y＝渐近线是又21ab2).44yx22＝－双曲线方程为oxy解：4,2)x21y4xN（的交于＝与渐近线＝点作直线过Q52,yx21y轴上在的上方，即双曲线焦点＝点在直线N1ba2222xy设双曲线方程为得到入上式代），把双曲线经过点（,)5,4(54,4,1)2),122ba解得由.4x4y22＝－双曲线方程为变题：已知双曲线渐近线是，并且双曲线过点02yx)5,4(N求双曲线方程。1b)5(a422221)x21y＝渐近线是又21ba2)NQ轴上。则焦点在若轴则双曲线的交点在中，若求得双曲线y,0;x,02222byax例4．已知双曲线的渐近线是，并且双曲线过点02yx),3,4(M求双曲线方程。.44yx22＝－所求双曲线方程为022yx双曲线的渐近线方程为：解.422yx为可设所求双曲线的方程)3,4(M双曲线过点.)3(44224练习题：的双曲线方程。且过点有相同渐近线，求与)3,4(14.222Myx的双曲线方程。且焦点为有相同渐近线，求与)0,5(14.322yx方程。的焦点为顶点的双曲线，且以椭圆求渐近线为1521y.422yxx1.求下列双曲线的渐近线方程：328).122yx819).222yx4).322yx12549).422yx)42(xy)3(xy)(yx)57(yx6、求中心在原点，对称轴为坐标轴，经过点P(1,－3)且离心率为的双曲线标准方程。25.过点（1，2），且渐近线为yx34的双曲线方程是________。,2,2222xy已知双曲线-=1(a>0,b>0)的离心率abe2,令双曲线两条渐近线构成的角中,以实轴为角平分思考线的夹角为试求的取值范题:围.