高中数学 141正弦函数、余弦函数的图像课件 新人教A版必修4 课件VIP免费

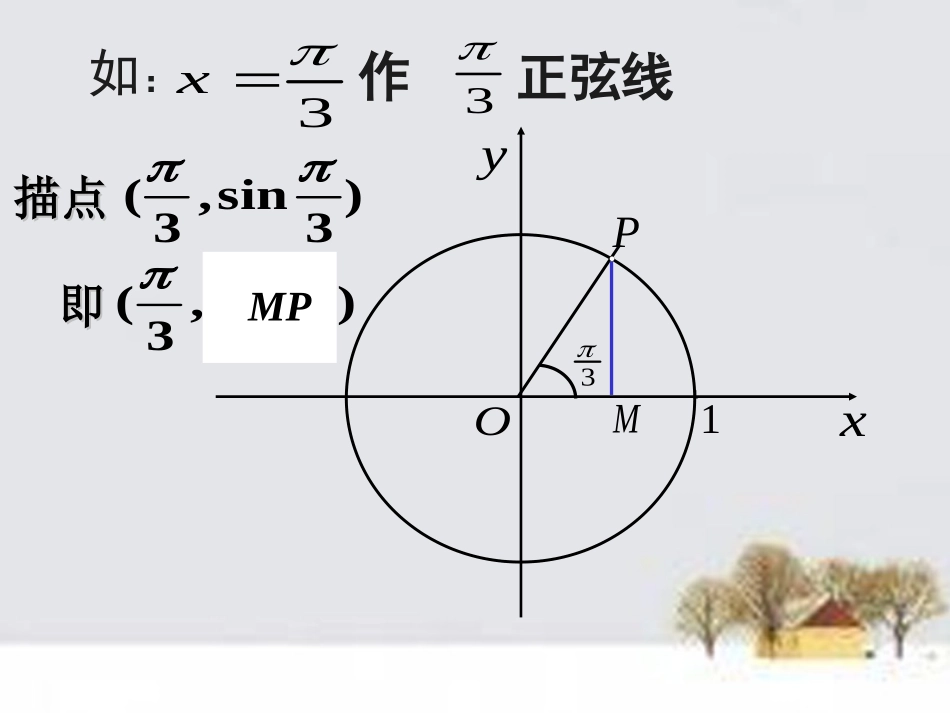
1.4.1正弦函数、余弦函数的图象新课讲授新课讲授1.函数图象的几何作法2,0sinxxy，由于在单位圆中，角x的正弦线表示其正弦值，因此可将正弦线移动到直角坐标系中确定对应的点（x,sinx）,从而作出函数图象.PM31Oxy1如：作正弦线3x3描点描点)3sin,3(即即)3sin,3(MP21oA步骤:(1)等分3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线作图过程演示oxy---11---1--函数的图象.2,0sinxxy，21oA步骤:(1)等分3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线作图过程演示想想：如何作出y=sinx在R上的图象？oxy---11---1--2o46246xy---------1-1问题：怎么在整个定问题：怎么在整个定义域义域RR范围作出正范围作出正弦函数的图像呢？弦函数的图像呢？因为sin(x+2kπ)=sinx,k∈Z,所以y=sinx在的图象与y=sinx,x∈[0,2π]的图象形状完全一样只是位置不同.2,(21),0kkk正弦曲线1.y=sinx在R上的图象想一想:余弦函数y=cosx在R上的图象又该如何作图?探索画图方法探索画图方法(1)、描点法(3)、利用图象平移法sin()2x发现问题：xycos余弦函数cos,yxxR与函数sin(),2yxxR是同一个函数；2余弦函数的图像可以通过正弦曲线向左平移各单位长度而得到．(2)、几何法（利用三角函数线）2.y=cosx在R上的图象32532522322322-11yx0sin,yxxRcos,yxxR余弦函数的图象正弦函数的图象y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同32532522322322-11yx032532522322322-11yx0sin,yxxRcos,yxxRy=cosx在R上的图象y=sinx在R上的图象图象的最高点(,1)2图象的最低点3(,1)2(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)3.五点法作：y=sinx、y=cosx,x∈[0,2π]图象.问题：图象中的关键点有哪些？及与x轴的交点(0,0)(,0)(2,0)与x轴的交点(0,0)(,0)(2,0)图象的最高点(,1)2图象的最低点3(,1)2与x轴的交点(,0)23(,0)2图象的最高点(0,1)(2,1)图象的最低点(,1)简图作法(五点作图法)(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)sin,[0,2]yxxcos,[0,2]yxx简图作法:(五点作图法)(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)例1画出下列函数的简图：（1）y=1+sinx，x[0,2]；（2）y=－cosx，x[0,2].（1）画出函数y=1+sinx，x[0,2]的简图.xsinx1+sinx22302010-1012101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]按五个关键点列表求值解:注：注：函数函数yy=1+sin=1+sinxx，，xx[0,2π]∈[0,2π]∈的图象可由函数的图象可由函数yy=sin=sinxx，，x[0,2π]∈x[0,2π]∈图象向上平移一个单位得到。图象向上平移一个单位得到。o1yx22322-12y=1+sinx解:按五个关键点列表求值按五个关键点列表求值描点作图02322xxcosxcos1-11-100-1100（2）画出函数y=－cosx，x[0,2]的简图......yy==－－coscosxxyy=cos=cosxx2322x1-1yO注：注：函数函数yy=-cos=-cosxx，，xx[0,2π]∈[0,2π]∈的图象与函数的图象与函数yy=cos=cosxx，，xx[0,2π]∈[0,2π]∈图象关于图象关于xx轴对称。轴对称。画出下列函数的简图:练习：，）（xysin120，x，）（xycos1220，x，）（xysin2320，x，）（xysin120，x解:02232xxsin0101022311yxO2xysin，）（xycos1220，x解:02232xxcos12101222312yxO2，）（xysin2320，x解:02232xxsin20202022311yxO222例2.画出下列函数的简图：（1）y=|sinx|;（2）y=|cosx|;（3...