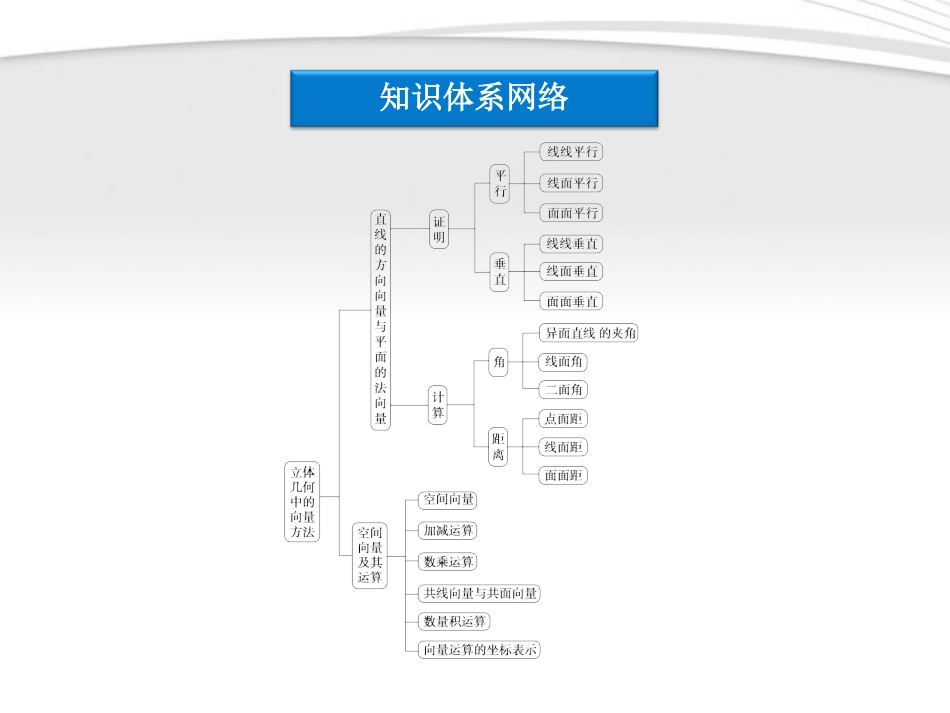
本章优化总结专题探究精讲本章优化总结知识体系网络知识体系网络专题探究精讲空间向量与空间位置关系题型特点:向量作为工具来研究几何,真正实现了几何中的形与代数中的数的有机的结合.给立体几何的研究带来了极大的便利,不论证明平行还是垂直,只需简单的运算就可以解决问题.知识方法:用向量方法证明平行与垂直问题的一般步骤是:(1)建立立体图形与空间向量的关系,利用空间向量表示问题中所涉及到的点、线、面,把立体几何问题转化为空间向量问题.(2)通过向量的运算研究平行或垂直关系,有时可借助于方向向量或法向量.(3)根据运算结果解释相关的问题.例例11已知正方体ABCDA1B1C1D1,求证:AD1∥平面BDC1.【证明】以D为坐标原点,建立如图所示的空间直角坐标系Oxyz.设正方体的棱长为1,则有D(0,0,0),A(1,0,0),D1(0,0,1),B(1,1,0),C1(0,1,1),AD1→=(-1,0,1),设n=(x,y,z)为平面BDC1的法向量,则n⊥DB→,n⊥DC1→.所以x,y,z·1,1,0=0,x,y,z·0,1,1=0.即x+y=0,y+z=0.令x=1,则n=(1,-1,1).n·AD1→=(1,-1,1)·(-1,0,1)=0,知n⊥AD1→.又AD1⊄平面BDC1,所以AD1∥平面BDC1.空间向量与空间角题型特点:空间角包括:异面直线所成的角(线线角);直线与平面所成的角(线面角);二面角(面面角),用向量法求空间角,就是把复杂的作角、证明、求角问题代数化,降低了思维难度,是近年来高考的一个方向.知识方法:(1)求异面直线所成的角设两异面直线的方向向量分别为n1、n2,那么这两条异面直线所成的角为θ=〈n1,n2〉或θ=π-〈n1,n2〉,∴cosθ=|cos〈n1,n2〉|.(2)求二面角的大小如图,设平面α、β的法向量分别为n1、n2.因为两平面的法向量所成的角(或其补角)就等于平面α、β所成的锐二面角θ,所成cosθ=|cos〈n1,n2〉|.(3)求斜线与平面所成的角如图,设平面α的法向量为n1,斜线OA的方向向量为n2,斜线OA与平面所成的角为θ,则sinθ=|cos〈n1,n2〉|.已知正方形ABCD所在的平面和矩形ACEF所在平面互相垂直,AB=2,AF=1.试在线段AC上确定一点P,使得PF与CD所成的角为60°.例例22【解】如图所示建立空间直角坐标系Cxyz,则F(2,2,1),CD→=(2,0,0).设P(t,t,0)(0≤t≤2),则PF→=(2-t,2-t,1). PF与CD所成的角是60°,∴cos60°=|2·2-t|2·2-t2+2-t2+1,解得t=22或t=322(舍去).∴当P为AC中点时,满足题设条件.如图,直三棱柱ABCA1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1B1.(1)证明:AB=AC;(2)设二面角ABDC为60°,求B1C与平面BCD所成的角的大小.例例33【解】(1)证明:以A为坐标原点,建立如图所示的空间直角坐标系Axyz.设B(1,0,0),C(0,b,0),D(0,0,c),则B1(1,0,2c),E(12,b2,c).(b>0,c>0)于是DE→=(12,b2,0),BC→=(-1,b,0).由DE⊥平面BCC1B1知DE⊥BC,DE→·BC→=0,求得b=1,∴AC→=(0,1,0),又AB→=(1,0,0),∴|AB→|=|AC→|,所以AB=AC.(2)设平面BCD的法向量AN→=(x,y,z),则AN→·BC→=0,AN→·BD→=0.又BC→=(-1,1,0),BD→=(-1,0,c),故-x+y=0-x+cz=0.令x=1,则y=1,z=1c,AN→=(1,1,1c).又平面ABD的一个法向量AC→=(0,1,0),由二面角ABDC为60°知,〈AN→,AC→〉=60°,故AN→·AC→=|AN→|·|AC→|·cos60°,求得c=12.于是AN→=(1,1,2),CB1→=(1,-1,2).因此cos〈AN→,CB1→〉=AN→·CB1→|AN→|·|CB1→|=12,〈AN→,CB1→〉=60°.所以B1C与平面BCD所成的角为30°.利用空间向量解决存在性问题题型特点:立体几何中的探索性、存在性问题,在命题中多以解答题的一步出现,试题有一定的难度.知识方法:存在性问题即在一定条件下论证会不会出现某个结论.这类题型常以适合某种条件的结论“存在”、“不存在”、“是否存在”等语句表述.解答这类问题,一般要先对结论作出肯定的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,若导致合理的结论,则存在性也随之解决;若导致矛盾,则否定了存在性.已知四棱锥PABCD的底面ABCD为等腰梯形,A...