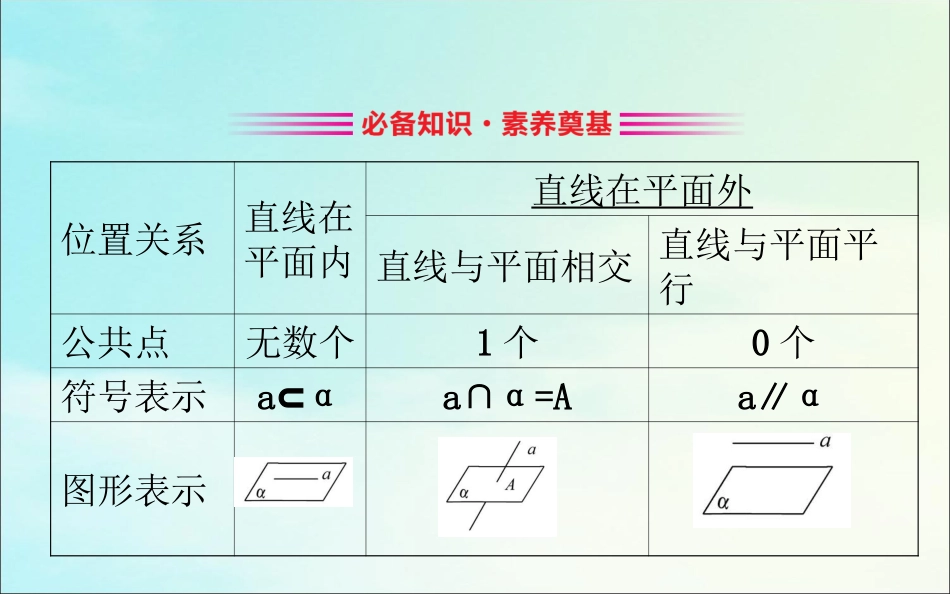
2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系位置关系直线在平面内直线在平面外直线与平面相交直线与平面平行公共点无数个1个0个符号表示a⊂αa∩α=Aa∥α图形表示【思考】“直线在平面外”与“直线与平面没有公共点”是相同的意义吗?提示:不相同.前者包括直线与平面平行及直线与平面相交这两种情况,而后者仅指直线与平面平行.2.平面与平面的位置关系位置关系平行相交图示表示法α∥βα∩β=a公共点个数0个无数个【素养小测】1.思维辨析(对的打“√”,错的打“×”)(1)若直线l上有无数个点不在平面α内,则l∥α.()(2)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.()(3)若平面α内的任意直线与平面β均无交点,则α∥β.()(4)若两个平面都平行于同一条直线,则这两个平面平行.()提示:(1)×.若直线l上有无数个点不在平面α内,则l∥α或直线l与平面α相交.(2)×.如果两条平行直线中的一条与一个平面平行,那么另一条与这个平面平行或在这个平面内.(3)√.由平面与平面平行的定义可知,此说法正确.(4)×.若两个平面都平行于同一条直线,则这两个平面平行或相交.2.三棱台的一条侧棱所在直线与其对面所在的平面之间的关系是()A.相交B.平行C.直线在平面内D.平行或直线在平面内【解析】选A.延长各侧棱恢复成棱锥的形状可知,三棱台的一条侧棱所在直线与其对面所在的平面相交.3.在以下三个命题中,正确的命题是()①平面α内有两条直线和平面β平行,那么这两个平面平行;②平面α内有无数条直线和平面β平行,则α与β平行;③在平面α,β内分别有一条直线,这两条直线互相平行,那么这两个平面平行或相交.A.①②B.②③C.③D.①③【解析】选C.如图所示,在正方体ABCD-A1B1C1D1中,对于①,平面AA1D1D中,AD∥平面A1B1C1D1,分别取AA1,DD1的中点E,F,连接EF,则EF∥平面A1B1C1D1,但平面AA1D1D与平面A1B1C1D1是相交的,交线为A1D1,故命题①错;对于②,平面AA1D1D中,与平面A1B1C1D1平行的直线有无数条,但平面AA1D1D与平面A1B1C1D1不平行,而是相交于直线A1D1,故命题②错.命题③是正确的.类型一直线与平面的位置关系【典例】1.(2019·丽水高一检测)下列命题错误的是()A.若直线l平行于平面α,则平面α内存在直线与l平行B.若直线l平行于平面α,则平面α内存在直线与l异面C.若直线l平行于平面α,则平面α内存在直线与l垂直D.若直线l平行于平面α,则平面α内存在直线与l相交2.下列说法中,正确的个数是()①如果两条平行直线中的一条和一个平面相交,那么另一条直线也和这个平面相交;②经过两条异面直线中的一条直线有一个平面与另一条直线平行;③两条相交直线,其中一条与一个平面平行,则另一条一定与这个平面平行.A.0B.1C.2D.33.如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是A1B1和BB1的中点,试判断(1)AM所在的直线与平面ABCD的位置关系?(2)CN所在的直线与平面ABCD的位置关系?(3)AM所在的直线与平面CDD1C1的位置关系?(4)CN所在的直线与平面CDD1C1的位置关系?【思维·引】1.由直线l平行于平面α知直线l与平面α无公共点,据此逐项判断.2.依据直线与平面的三种位置关系的定义逐项判断.3.依据直线与平面的三种位置关系的定义和正方体的结构特征逐项判断.【解析】1.选D.若直线l平行于平面α,则平面α内的直线与l平行或异面,故A,B正确;在C中,若直线l平行于平面α,则平面α内存在直线与l异面垂直,故C正确;在D中,若直线l平行于平面α,则平面α内的直线与l平行或异面,故D错误.2.选C.易知①正确,②正确.③中两条相交直线中一条与平面平行,另一条可能平行于平面,也可能与平面相交,故③错误.3.(1)AM所在的直线与平面ABCD相交.(2)CN所在的直线与平面ABCD相交.(3)AM所在的直线与平面CDD1C1平行.(4)CN所在的直线与平面CDD1C1相交.【类题·通】直线与平面位置关系的判断(1)以正方体为模型,将线面化归成正方体中的线面进行判断.(2)以身边的物体作为模型判断,如笔,墙角作为直线,桌面,墙面,地面作为平面.提醒:在判断直线与平面的位置关系时,三种情形都要考虑到,避免疏忽或遗漏.【习练·破】在长方体ABCD-A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D1、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1C...