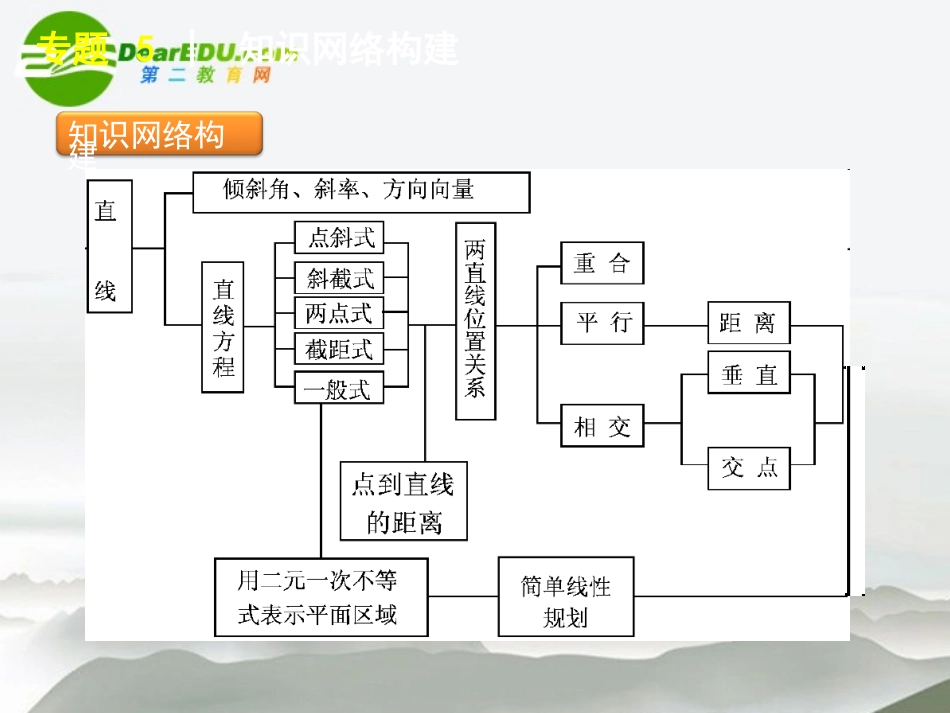
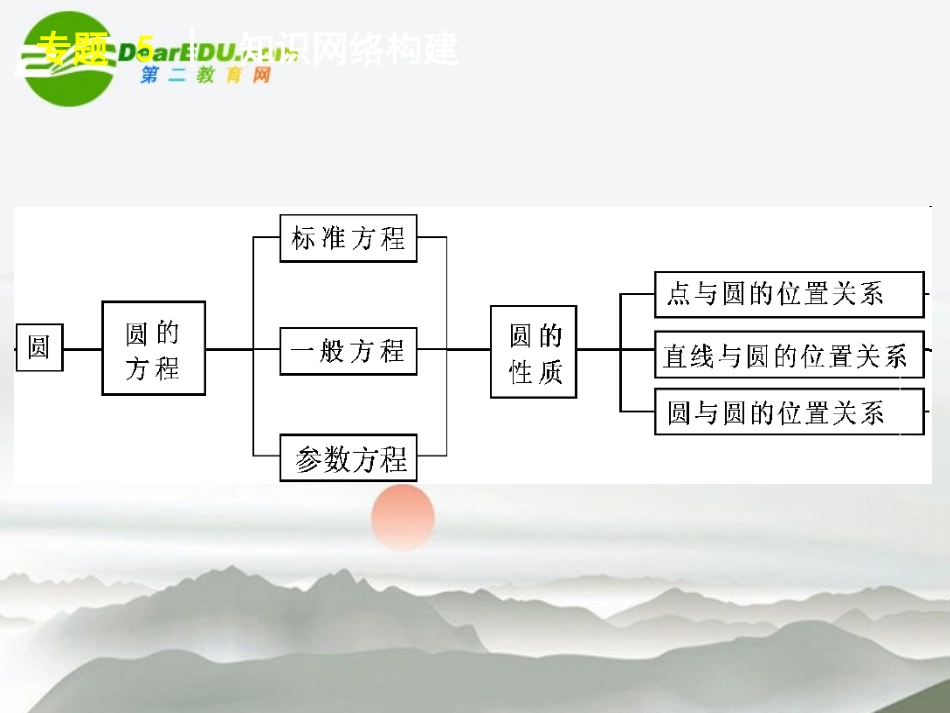
专题5平面解析几何知识网络构建专题5│知识网络构建专题5│知识网络构建专题5│知识网络构建考情分析预测专题5│考情分析预测1.三年高考回顾年份内容题号与分值2008直线与方程椭圆与圆综合圆的方程第8题5分;第12题5分;第18题16分.2009椭圆综合直线与圆综合第13题5分;第18题16分.2010双曲线直线与圆椭圆综合第6题5分;第9题5分;第18题16分.专题5│考情分析预测2.命题特点探究近三年江苏试题特点:①一般是两个填空题和一个解答题,分值26分左右;②关注解析几何本质知识的考查,很少与其他知识交汇,比如和三角向量交汇等;③解答题中研究变化之中不变的量(含参数方程恒成立问题)问题受到青睐;④试题运算量大,区分度高.专题5│考情分析预测3.命题趋势预测2011年江苏高考对解析几何的考查仍然会坚持前几年的原则不变,需要关注以下几个问题:①求直线方程和圆的方程、研究直线与圆的位置关系仍然是考试命题的主要来源.②圆锥曲线(主要是椭圆)中的定义、离心率、焦点三角形等知识一般是填空题的中高档试题,有一定的难度,计算量有时会比较大,而且方法比较灵活,复习时要注意多加强这方面的训练.③试题会突出解析几何问题的几何特征,让学生用几何的眼光看待解析几何问题,关注能力(特别是运算能力)的考查.④在研究直线(点)与圆的位置关系时,先套上一个简单的椭圆问题,这一类型的问题值得关注.第第1010讲直线与圆讲直线与圆第10讲│直线与圆主干知识整合第10讲│主干知识整合1.平行与垂直若直线l1和l2有斜截式方程l1:y=k1x+b1,l2:y=k2x+b2,则(1)直线l1∥l2的充要条件是k1=k2且b1≠b2.(2)直线l1⊥l2的充要条件是k1·k2=-1.若l1和l2都没有斜率,则l1与l2平行或重合.若l1和l2中有一条没有斜率而另一条斜率为0,则l1⊥l2.2.对称问题(1)点关于点成中心对称的对称中心恰是以这两点为端点的线段的中点,因此中心对称的问题是线段中点坐标公式的应用问题.设P(x0,y0),对称中心为A(a,b),则P关于A的对称点为P′(2a-x0,2b-y0).第10讲│主干知识整合(2)点关于直线成轴对称问题由轴对称定义知,对称轴即为两对称点连线的“垂直平分线”.利用“垂直”、“平分”这两个条件建立方程组,就可求出对称点的坐标.一般情形如下:设点P(x0,y0)关于直线y=kx+b的对称点为P′(x′,y′),则有y′-y0x′-x0·k=-1,y′+y02=k·x′+x02+b,可求出x′、y′.特殊地,点P(x0,y0)关于直线x=a的对称点为P′(2a-x0,y0);点P(x0,y0)关于直线y=b的对称点为P′(x0,2b-y0).第10讲│主干知识整合(3)曲线关于点、曲线关于直线的中心或轴对称问题,一般是转化为点的中心对称或轴对称(这里既可选特殊点,也可选任意点实施转化).一般结论如下:曲线f(x,y)=0关于已知点A(a,b)的对称曲线的方程是f(2a-x,2b-y)=0.第10讲│主干知识整合(4)曲线f(x,y)=0关于直线y=kx+b的对称曲线的求法:设曲线f(x,y)=0上任意一点为P(x0,y0),P点关于直线y=kx+b的对称点为P′(x,y),则由(2)知,P与P′的坐标满足y-y0x-x0·k=-1,y0+y2=k·x0+x2+b,从中解出x0、y0,代入已知曲线f(x,y)=0,应有f(x0,y0)=0.利用坐标代换法就可求出曲线f(x,y)=0关于直线y=kx+b的对称曲线方程.第10讲│主干知识整合3.圆的方程圆的一般方程x2+y2+Dx+Ey+F=0(*)体现了圆方程的代数特点:x2、y2项系数相等且不为零,没有xy项.当D2+E2-4F=0时,方程(*)表示点-D2,-E2,当D2+E2-4F<0时,方程(*)不表示任何图形.4.点与圆的位置关系点P(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系有三种:若d=a-x02+b-y02,则d>r⇔点P在圆外;d=r⇔点P在圆上;dr⇔相离⇔Δ<0;d=r⇔相切⇔Δ=0;d0.其中d=|Aa+Bb+C|A2+B2.6.两圆位置关系的判定方法设两圆圆心分别为O1,O2,半径分别为r1,r2,|O1O2|=d.d>r1+r2⇔外离⇔4条公切线;d=r1+r2⇔外切⇔3条公切线;|r1-r2|