高中数学 第二章 平面解析几何初步 221 直线方程的几种形式课件 新人教B版必修2 课件VIP免费

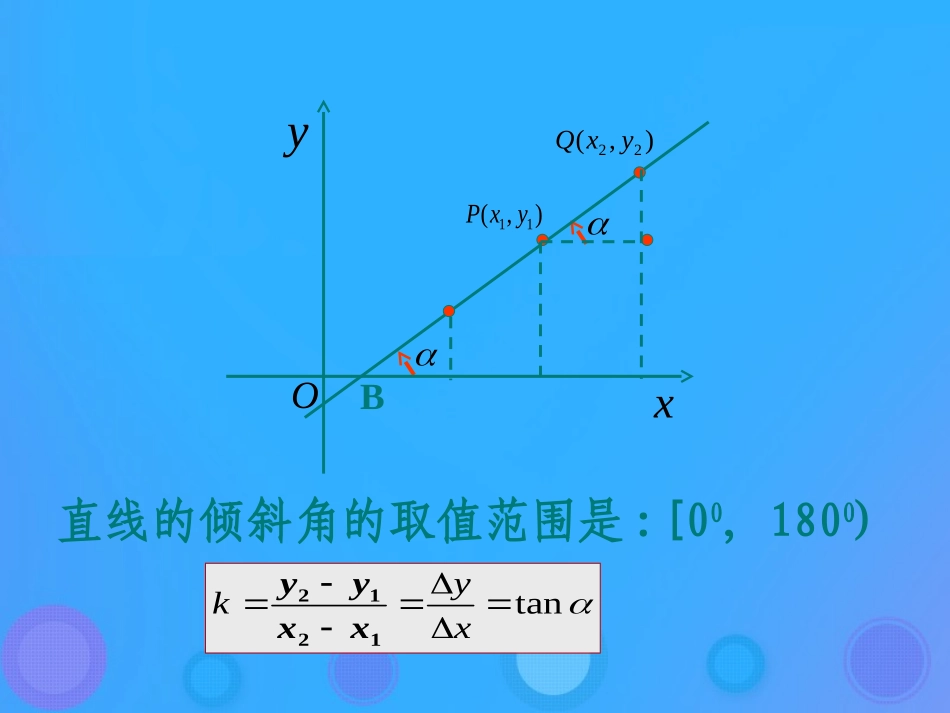
2.2.2直线的点斜式方程复习.,),,(),,(2.122211的斜率那么直线如果已知直线上两点PQxxyxQyxP1.倾斜角的定义及其取值范围;xyO),(22yxQ),(11yxP直线的倾斜角的取值范围是:[00,1800)Btanxyk1212xxyy在平面直角坐标系内，如果给定一条直线经过的一个点和斜率，能否将直线上所有的点的坐标满足的关系表示出来呢？000,yxPlkyx,xyOlP0，00xxyyk00xxkyy直线经过点，且斜率为，设点是直线上不同于点的任意一点，因为直线的斜率为，由斜率公式得：000,yxPkyxP,0Plk即：xyOlP0P（1）过点，斜率是的直线上的点，其坐标都满足方程吗？00xxkyy000,yxPkl（2）坐标满足方程的点都在过点，斜率为的直线上吗？00xxkyy000,yxPkl经过探究，上述两条都成立，所以这个方程就是过点，斜率为的直线的方程．k000,yxPl00xxkyy方程由直线上一点及其斜率确定，把这个方程叫做直线的点斜式方程，简称点斜式（pointslopeform）．直线的点斜式方程直线的点斜式方程xyOlP0kl的斜率为直线（1）轴所在直线的方程是什么？x00yy0yy，或当直线的倾斜角为时，即．这时直线与轴平行或重合，ll000tanxxyOl0Pl的方程就是坐标轴的直线方程坐标轴的直线方程故轴所在直线的方程是:x0y（2）轴所在直线的方程是什么？y00xx0xx，或当直线的倾斜角为时，直线没有斜率，这时直线与轴平行或重合，它的方程不能用点斜式表示．这时，直线上每一点的横坐标都等于，所以它的方程就是ll90ly0xxyOl0P坐标轴的直线方程坐标轴的直线方程0x故轴所在直线的方程是：y求下列直线的方程:12,1k1l(1)直线：过点（），22,1l(2)直线：过点（-）和点（3，-3）如果直线的斜率为，且与轴的交点为，代入直线的点斜式方程，得：lyk0xkbyb,0也就是：bkxyxyOl0Pb我们把直线与轴交点的纵坐标b叫做直线在轴上的截距（intercept）．y该方程由直线的斜率与它在轴上的截距确定，所以该方程叫做直线的斜截式方程，简称斜截式（slopeinterceptform）．y直线的斜截式方程直线的斜截式方程观察方程，它的形式具有什么特点？bkxy1、我们发现，左端的系数恒为1，右端的系数和常数项均有明显的几何意义：byxkkb是直线的斜率，是直线在轴上的截距．y2、斜截式是点斜式的特例，只适用于斜率存在的情形。3、直线在坐标轴上的横、纵截距及求法：截距的值是实数，它是坐标值，不是距离4、方程与我们学过的一次函数的表达式类似．我们知道，一次函数的图象是一条直线．你如何从直线方程的角度认识一次函数？一次函数中和的几何意义是什么？bkxybkxykb5、你能说出一次函数及图象的特点吗？xyxy3,123xy1,12求过点（0）,斜率为-的直线的方程.思考：大家都知道：两点确定一条直线！那么经过两个定点的直线的方程能否用“公式”直接写出来呢？二、问题的提出：三、师生探究(一):直线的两点式方程合作学习1：设直线l经过两点P1(x1，y1)，P2(x2，y2)，其中x1≠x2，y1≠y2，则①直线l斜率是什么？②你能写出直线l的点斜式方程吗？结论:(1)斜率(2)方程写成比例式可化为_____________.设直线l经过两点P1(x1,y1),P2(x2,y2),其中x1≠x2，y1≠y2，求l的方程.展示：1212xxyyK211121()yyyyxxxx展示：设直线l经过两点P1(x1,y1),P2(x2,y2),其中x1≠x2，y1≠y2，求l的方程.结论:方程化成比例式为：(x1≠x2且y1≠y2)此方程叫做直线的两点式方程。211121()yyyyxxxx112121yyxxyyxx说明(1)这个方程由直线上两点确定;(2)当直线没有斜率或斜率为0时,不能用两点式求出它们的方程.(此时方程如何得到?)ABxyoCM典例分析1：已知三角形的三个顶点A（-4，0），B（2，-4），C（0，2），求AC边所在直线的方程，以及BC边上中线所在直线的方程。3.72xl例2：求下列直线的方程：1已知直线l的斜率为，在轴上的截距是求的方程。2.A,B是x轴上的两点，点P的横坐标为2且PA=PB,直线PA的方程为x-y+1=0,求直线PB的方程例3若两点是直线l与x轴的交点A(a,0),与y轴的交点B(0,b),其中a≠0,b≠0,则直线l的方程是怎样...