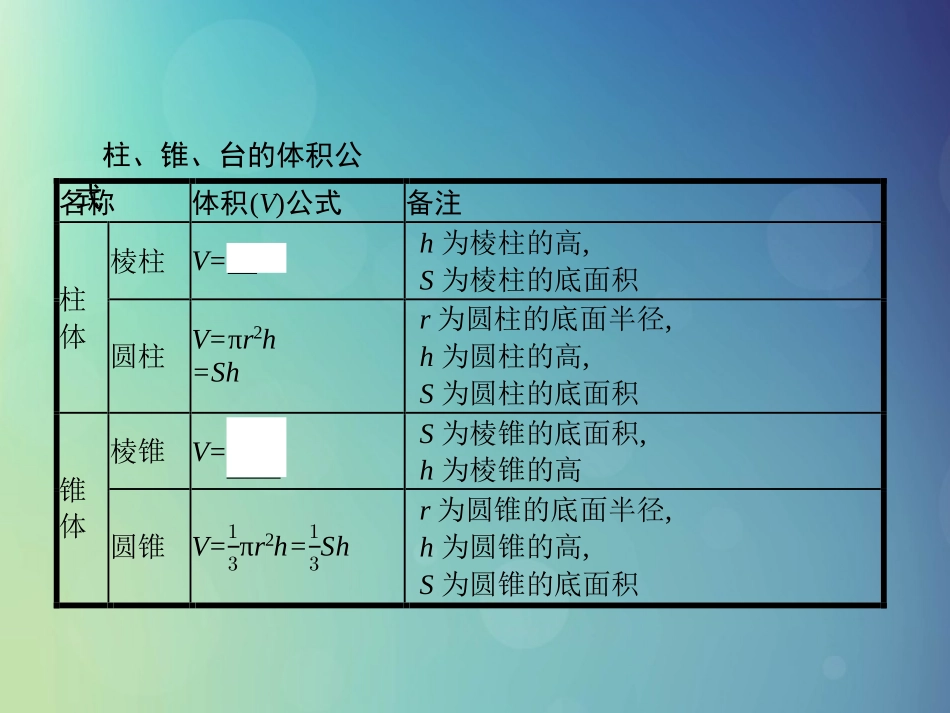
7.2柱、锥、台的体积1.掌握柱、锥、台的体积公式及求法.2.能运用公式求解柱体、锥体和台体的体积,并熟悉台体与柱体及锥体之间的转换关系.名称体积(V)公式备注柱体棱柱V=Shh为棱柱的高,S为棱柱的底面积圆柱V=πr2h=Shr为圆柱的底面半径,h为圆柱的高,S为圆柱的底面积锥体棱锥V=13ShS为棱锥的底面积,h为棱锥的高圆锥V=13πr2h=13Shr为圆锥的底面半径,h为圆锥的高,S为圆锥的底面积柱、锥、台的体积公式名称体积(V)公式备注台体棱台V=13(S上+S下+ටS上·S下)hS上,S下分别为棱台上、下底面的面积,h为棱台的高圆台V=13πh(r2+rr'+r'2)=13(S上+S下+ටS上·S下)hr,r'分别为圆台上、下底面的半径,h为圆台的高,S上,S下分别为圆台上、下底面的面积柱体和锥体可以看作是由台体变化得到的.柱体可以看作是上、下底面全等的台体,锥体可以看作是上底面缩小成一点的台体,因此,很容易得出它们的体积公式间的关系:【做一做1】已知圆柱OO'的高为5,底面直径为4,则圆柱OO'的体积为()A.20B.10C.20πD.80π答案:C【做一做2】已知五棱锥的高为10,底面积为3,则其体积为()A.30B.10C.3D.1答案:B【做一做3】已知圆锥的底面半径为1,高为2,则圆锥的体积为()A.B.2πC.4πD.6π答案:A2𝜋3【做一做4】已知圆台的上、下底面半径分别是2,4,高是3,则该圆台的体积是()答案:A【做一做5】在正四棱台ABCD-A'B'C'D'中,AB=2,A'B'=6,体积V=112,求该正四棱台的高.解设该正四棱台的高为h,A.28πB.6+2ξ2C.20πD.6π则有13×(22+62+ξ22×62)h=112,解得h=8413,即该正四棱台的高为8413.题型一题型二题型三题型四题型一求柱体的体积【例1】如图①是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②所示.求正三棱柱ABC-A1B1C1的体积.分析:由主视图可以得到正三棱柱的底面三角形的高和侧棱长.题型一题型二题型三题型四反思求柱体的体积的关键是求底面积和高,而底面积的求解要根据平面图形的性质灵活处理.熟记常见平面图形的面积的求法是解决此类问题的关键.解:由主视图可知,在正三棱柱中,AD=ξ3,AA1=3,从而在等边三角形ABC中,BC=AB=𝐴𝐷sin60°=ξ3ඥ32=2,所以正三棱柱的体积V=Sh=12·BC·AD·AA1=12×2×ξ3×3=3ξ3.题型一题型二题型三题型四【变式训练1】一个正方体和一个圆柱等高,并且侧面面积相等,则这个正方体和圆柱的体积之比为.解析:由于正方体和圆柱等高,故可设正方体的棱长和圆柱的高(母线长)都为a,设圆柱的底面半径为r,则正方体的侧面面积为4a2,圆柱的侧面面积为2πra,又4a2=2πra,所以r=2πa,所以正方体的体积V正方体=a3,圆柱的体积V圆柱=πr2a=4πa3,故𝑉正方体𝑉圆柱=π4.答案:π4题型一题型二题型三题型四题型二求锥体的体积【例2】一个正三棱锥的底面边长为6,侧棱长为,求这个正三棱锥的体积.分析:已知底面边长和侧棱长,可先求出三棱锥的底面积和高,再根据体积公式求出其体积.ξ15题型一题型二题型三题型四解:如图所示为正三棱锥S-ABC.设H为正三角形ABC的中心,连接SH,则SH的长即为该正三棱锥的高.连接AH并延长交BC于点E,则E为BC的中点,且AE⊥BC. △ABC是边长为6的正三角形,∴AE=ξ32×6=3ξ3.∴AH=23AE=2ξ3.在△ABC中,S△ABC=12BC·AE=12×6×3ξ3=9ξ3.在Rt△SHA中,SA=ξ15,AH=2ξ3,∴SH=ට𝑆𝐴2-𝐴𝐻2=ට15-12=ξ3.∴V正三棱锥=13S△ABC·SH=13×9ξ3×ξ3=9.题型一题型二题型三题型四反思求锥体的体积,首先要选择适当的底面和高,然后应用公式V=Sh进行计算即可,常用方法为割补法和等积变换法:(1)割补法:求一个几何体的体积可以将这个几何体分割成几个柱体或锥体,分别求出柱体或锥体的体积,从而得出该几何体的体积.(2)等积变换法:利用三棱锥的任一个面可作为三棱锥的底面,可通过多种方式求其体积.①求体积时,可选择容易计算的方式来计算;②利用“等积性”可求“点到面的距离”.13题型一题型二题型三题型四【变式训练2】两个圆锥的母线长相等,侧面展开图扇形圆心角分别为120°和240°,体积分别为V1和V2,则V1∶V2等于()答案:CA.1∶8B.1∶10C.ξ10∶10D.ξ5∶5解析:设这两个圆锥的母线长均为l,底面半径分别为r1,r2,高分别为h1,h2,则120°=𝑟1𝑙·360°,240°=𝑟2𝑙·360°,所以r1=13l,r2=23l.所以...