高中数学(空间向量的数量积运算)课件 新人教版选修2-1 课件VIP免费

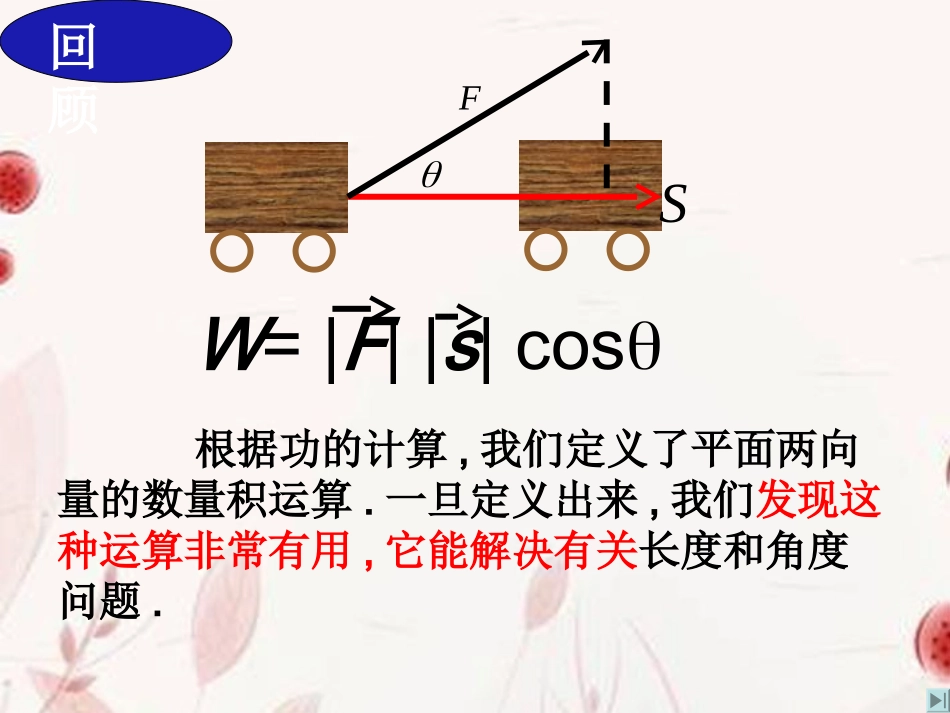
S�F�W=|F||s|cos根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.回顾1)两个向量的夹角的定义:OABaabb如图,已知两个非零向量、ab,在空间任取一点O,作OAa�,OBb�,则角AOB叫做向量a与b的夹角,记作:,ab.⑴范围:0,ab≤≤.,ab=0时,ab与同向;,ab=π时,ab与反向.⑵,,abba＝，⑶如果,2ab,则称a与b垂直,记为ab知新类似地，可以定义空间向量的数量积两个向量的夹角是惟一确定的！2）两个向量的数量积注:①两个向量的数量积是数量，而不是向量;②规定:零向量与任意向量的数量积等于零.已知空间两个非零向量、ab,则cos,abab叫做、ab的数量积,记作ab.即cos,ababab.abA1B1BA类比平面向量,你能说出ab的几何意义吗?如图11AB�是b在a方向上的射影向量.abA1B1BAab的几何意义数量积等于的长度与在的方向上的投影的乘积.baaabacosb显然,对于非零向量、ab,e是单位向量有下列性质:①cos,aeaae；②0;abab③2aaa也就是说2aa.3)空间两个向量的数量积性质注：性质②是证明两向量垂直的依据；性质③是求向量的长度（模）的依据.注：性质②是证明两向量垂直的依据；性质③是求向量的长度（模）的依据.4)空间向量的数量积满足的运算律⑴()()abab⑵abba(交换律)⑶()abcabac(分配律)注：向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立。注：向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立。如果不能，请举出反例能得到吗？由,对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量,,abcbacacb.不能，例如向量与向量都垂直时，有而未必有acb,,caba.cb不能，向量没有除法.对于三个均不为0的数若则对于向量若能否写成也就是说向量有除法吗？,,,cba,cab).(acbbca或,,bakba?)(akbbka或不成立，左边是一个与向量c共线的向量，右边是一个与向量a共线的向量，而向量c与a连是否共线都是一个未知数.对于三个均不为0的数对于向量成立吗？也就是说，向量的数量积满足结合律吗？,,,cba).()(bcacab若,,,cba)()(cbacba222222)()()()3)()()4)()abcabcpqpqpqpqpq��1.222,,22abab已知,则ab与的夹角大小为_____.2.判断真假:1)若0,ab则0,0ab()1353.设a,b,c是任意的非零空间向量,且相互不共线,则：①(a·b)c(c·a)b=0②|a|-|b|<|ab|③(b·c)a(c·a)b不与c垂直④(3a+2b)·(3a2b)=9|a|2-4b2中,真命题是()(A)①②(B)②③(C)③④(D)②④DADFCBE1(2)(3)(4)��图间边条边对线长点别点计（）3.如：已知空四形的每和角都等于1，、分是、的中。算：ABCDEFABADEFBAEFBDEFDCEFAC4.D'C'B'DABCA'解：ACABADAA�22222222||()||||||2()4352(0107.5)85.ACABADAAABADAAABADABAAADAA���||85.AC�ABCDABCD4AB3,5,90,60ADAABADBAADAAACP92.25.已知线段、在平面内，，线段如果，求、之间的距离.ABBDBDABAC,,ABaBDbACcCDcabCABD解： 22222222||()||||||CDCAABBDCAABBDabc��222CDabcP92.3法一:发现22222()ababab��代入求得.5.已知向量,ab��满足1,2,3abab��,则ab��_____.1法二:由2222abaabb��代入求得ab��=-2.∴2222abaabb��得ab��1法三:数形结合法,发现形的特...