高二数学必修五数列的概念及简单表示课件 苏教版 课件VIP免费

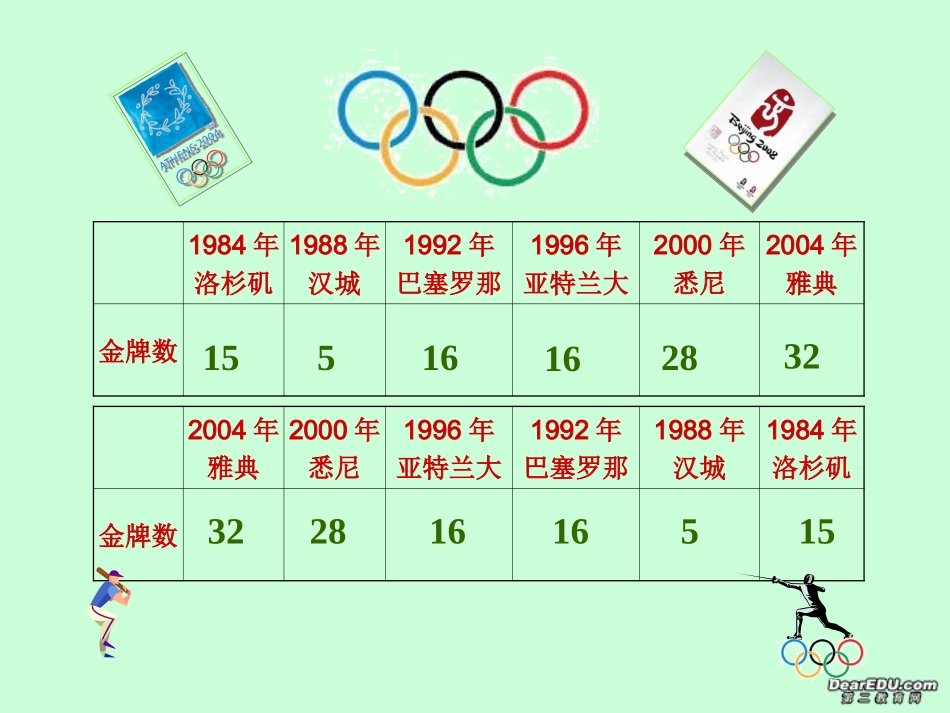
456781567812334264个格子1223344551667788你想得到什么样的赏赐？陛下，赏小人一些麦粒就可以。OK请在第一个格子放1颗麦粒请在第二个格子放2颗麦粒请在第三个格子放4颗麦粒请在第四个格子放8颗麦粒依次类推…456781456781233264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的2倍且共有64格子1??1844,6744,0737,0955,16152223212026322004年雅典2000年悉尼1996年亚特兰大1992年巴塞罗那1988年汉城1984年洛杉矶金牌数1984年洛杉矶1988年汉城1992年巴塞罗那1996年亚特兰大2000年悉尼2004年雅典金牌数1551616283215516162832共同特点共同特点：1.都是一列数；2.都有一定的次序236312222，，，，，15516162832，，，，，上述棋盘中各格子里的麦粒数按先后次序排成一列数：我国从2004年到1984年的6次奥运会上，各次参赛获得的金牌总数排成的一列数：我国从1984年到2004年的6次奥运会上，各次参赛获得的金牌总数排成的一列数：-1的1次幂，2次幂，3次幂，…排列成一列数：无穷多个1排列成的一列数：11111，，，，，11111，，，，，1234532281616515，，，，，25/2/24上午08:271.定义：请问，是不是同一数列？请问，是不是同一数列？(数列具有有序性)例1：数列改为315516162832，，，，，5162832，，，，，15164例2：数列改为11111，，，，，…11111，，，，，…按照一定次序排列的一列数叫做曰：“一尺之棰，日取其半，万世不竭.”庄子你能用一个数列来表达这句话的含义吗？1111124816，，，，，…1234512345，，，，，…15516162832，，，，，236312222，，，，…，11111，，，，，…11111，，，，，…各项依次叫做这个数列的第1项，第2项，···，第n项，···2、数列中的每个数叫做这个数列的项．3、数列的分类按项数分：项数有限的数列叫有穷数列项数无限的数列叫无穷数列有穷数列无穷数列有穷数列无穷数列无穷数列按照项与项之间的大小关系来分：递增数列、递减数列、摆动数列、常数列4.数列的一般形式可以写成：123naaaa，，，…，，…na是数列的第n项．12345222632112n，，31224……6111111，，，，，，，，，，，，，，，第1项1()nna12n64*(N,)nn1a第2项第3项3a2ana第n项n，，1，，-1n，，0212n的第n项na5、如果数列与序号n之间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的通项公式．12nnanna1na*(N)n简记为na其中是数1a列的第1项或称为首项,2n，，2nna解：首项为21111a22132a3a2315第2项为第3项为通项公式的作用例1：已知数列{an}的通项公式为an=2n－1，写出这个数列的首项、第2项和第3项．显然,有了通项公式,只要依次用1,2,3,…代替公式中的n,就可以求出这个数列的各项设某一数列的通项公式为)1(nnan123426122020以内的正奇数按从小到大的顺序构成的数列2311013519也就是说每个序号也都对应着一个数（项）序号项从函数的观点看，是的函数。y=f(x)ann函数值自变量数列项序号（正整数或它的有限子集）项6、数列的实质序号项即，数列可以看成以正整数集(或它的有限子集{1，2，…，n})为定义域的函数，当自变量从小到大的顺序依次取值时，所对应的一列函数值。序号通项公式从映射的观点看，数列可以看作是：序号到数列项的映射数列{an}与集合的区别：（1）集合中元素是无序的，而数列中的项必须按一定顺序排列，必须是有序的。（2）集合中的元素是互异的，而数列中的项可以是相同的。例2：已知数列{an}的通项公式，写出这个数列的前5项，并作出它们的图象．（1）na1;nn（2）na12.nn（1）na1nnna1nnn123451223344556onan1234560.10.30.50.70.9我们好孤单！是一些孤立点·····数列用图象表示时的特点——一群孤立的点123456on0.10.3-0.5-0.1-0.3anna12nnn12345121418116132（2）na12nn是一些孤立点·····分析：例3：写出下面数列的一个通项公式，使它的前4项分别是下列各数：1111112233445(),,,12341111111-...